Es wurden mehrere Tests mit jeweils vielfacher Wiederholung mit den nachfolgend aufgelisteten Funktionen vorgenommen, um Qualitätsunterschiede feststellen zu können. Die Testausgaben sind hier nicht alle dargestellt.
spritz_rand(): 2480ms s arc4random_uniform(): 13532ms s (~35s) random(): 348ms - rand(): 1567ms - lrand48(): 554ms -
Die zweite Funktion braucht in Wirklichkeit fast 3-mal länger als angegeben. Sie scheint irgendwie die Zeitnahme zu beeinflussen. Die mit s gekennzeichneten Funktionen führen einen automatischen Seed (Saat) durch. Jede Funktion hat 100.000.000 Zufallszahlen 0··255 generiert, die gespeichert wurden. Die vorstehenden Zeitwerte stammen von diesem Vorgang.
Die hier verwendete Spritz-Funktion enthält einen Hybrid-Generator.
Das bedeutet, daß sie deterministisch Zufallszahlen generiert, jedoch
durch einen nicht-deterministischen Seed gestartet
und immer wieder neu gestartet wird.
Die ausgegebenen Zufallszahlen sind daher nicht vorhersagbar.
Desweiteren ist Spritz eine kryptographische Funktion.
Dies erfordert, daß die ausgegebene Zahlenfolge nicht von einer echten
Zufallszahlenfolge unterscheidbar sein darf, und es darf nicht möglich sein,
anhand der Ausgabe auf den internen Zustand zu schließen, auch wenn die
genaue Funktionsweise bekannt ist.
Die Sequenz der ausgegebenen Zufallszahlen nach einem Seed darf sehr lang sein.
Eine Dokumentation beschreibt, daß etwa 2⁸¹ Ausgabe-Byte nötig sind, damit
eine sinkende kryptographische Qualität bemerkbar wird.
Zum vorzüglichen Algorithmus Rabbit wird hier eine Sequenzlänge
von 2⁶⁸ Byte angegeben.
RC4 ≠ Spritz:
steps: 2²⁴¹ ≠ 2¹²⁴⁷
states: N²N! ≠ N⁶N!
Spritz ist als Nachfolger dem RC4 haushoch überlegen, was
nicht nur durch die vorstehenden Unterschiede bewirkt wird.
Spritz basiert (weniger dominierend) wie Keccak (sha3) auf dem
Verhalten eines Schwamms (Aufsaugen/Auswringen).
Die Generatoren rand(), random(), lrand(), ...
sind Kongruenzgeneratoren und gehören zu den
im stochastischen Sinn Wenig bis nicht zuverlässigen Generatoren.
x spritz arc4 lrand48 random rand 0 176 174 8648 171 188 1 983 1002 0 1000 1157 2 2950 2988 229 3094 3239 3 6004 5902 11166 5881 6199 4 8865 8945 9 8925 8768 5 10607 10520 683 10534 10374 6 10472 10632 16955 10530 10236 7 8915 8913 29 8983 8658 8 6663 6589 1556 6707 6449 9 4582 4526 25416 4495 4432 10 2682 2644 3 2604 2720 11 1424 1441 40 1388 1572 12 726 703 802 680 817 13 284 329 0 333 405 14 134 131 0 121 200 15 46 73 0 60 73 16 17 12 0 21 38 17 5 9 0 7 8 18 1 2 0 2 1 19 0 1 0 0 1
Es wurden 3 Byte lange Sub-Strings von-bis
0xff0000··0xffffff generiert.
Alle diese Strings wurden in den
108 Zufallszahlen gesucht.
Erklärung anhand von 6 10472:
Es wurden 10472 verschiedene Sub-Strings jeweils 6-mal gefunden.
Die Anzahl Zahlen in 3 Bytes beträgt 224 = 16777216.
Die Division 100000000/16777216 = 5,96 macht klar, weshalb
die meisten Sub-Strings 5-mal oder 6-mal gefunden wurden.
Die Funktion lrand48() fällt überraschend vollkommen aus dem Rahmen!
Aber nur bei diesem Test.
Das nachfolgende Diagramm basiert auf den vorstehenden Zahlenreihen.
Bis auf die letzte Funktion wurde Spline-Interpolation verwendet.
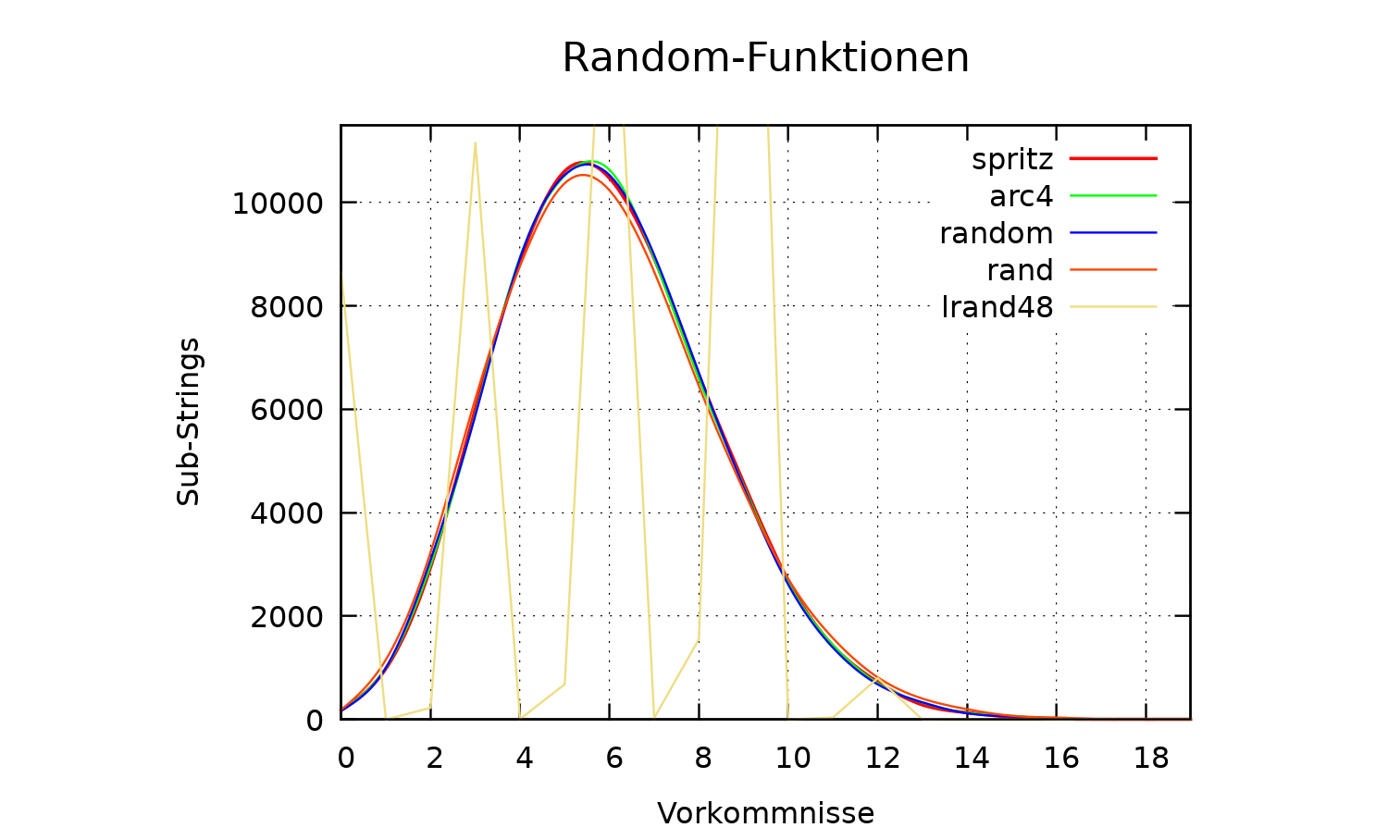
Es ist eine zwar leicht verzerrte, aber doch typische Glockenkurve zu sehen. Überraschend ist, daß alle Kurven (bis auf die krasse Ausreißerin) übereinander liegen. Zwischen den Kurven der ersten vier Funktionen sind nur vernachlässigbar geringe Unterschiede sichtbar. Qualitätsunterschiede sind mit den hier angewandten Mitteln somit nicht feststellbar. Die Verzerrung rührt daher, daß die x-Skale grob gestuft ist und wenig Teilstriche enthält, wegen der geringen Anzahlen von Vorkommnissen. Und weniger als 0 Vorkommnisse kann es nicht geben.
Sub-Strings Länge 4 0 4008 1 90 2 1 Sub-Strings Länge 5 0 4098 1 1
Drei Byte lange Sub-Strings gibt es viele (s.o.), jedoch bei Längen von 4 und 5 geht deren gefundene Anzahl gegen 0.
Mittelwert=127.504896 Mw=127.501873 n=20292 i=20292 ng=1 Mw=127.502622 n=221932 i=242224 ng=2 Mw=127.508347 n=18450 i=260674 ng=3 Mw=127.508698 n=1172141 i=1457987 ng=5 Mw=127.505290 n=71268 i=1529255 ng=6 Mw=127.508787 n=7636888 i=9166143 ng=7 Mw=127.501001 n=30135652 i=41692474 ng=15 Mw=127.502722 n=49047 i=41741521 ng=16 Mw=127.501014 n=12813083 i=54554604 ng=17 Mw=127.503746 n=21888 i=54576492 ng=18 Mw=127.501002 n=27154162 i=82490110 ng=37 Mw=127.502277 n=82783 i=82572893 ng=38 Mw=127.502869 n=21439 i=82594332 ng=39 Mw=127.508299 n=249477 i=82954478 ng=43
Vorstehend wurden Zeilen gelöscht, was an ng=# erkennbar ist.
Es wurden die periodischen Annäherungen an den zuvor errechneten Mittelwert
geprüft, ohne signifikante Unterschiede zwischen den Funktionen
feststellen zu können.
Die Funktionen verhalten sich untereinander gleich, egal, welche Parameter
des testenden Algorithmus wie stark verändert werden.
Bei 100 Millionen Zahlen kommen Sequenzen vor, in denen über 30 Millionen
Prüfungen erfolglos bleiben, bis eine Annäherung geschafft wird.
Die Parameter können derartig verändert werden, sodaß erfolgreiche Vorkommnisse
erst nach mehr als 70 Millionen geprüfter Zahlen vorliegen.
Der Mittelwert beträgt (0+255)/2 = 127,5 rechnerisch. Die gemessenen Mittelwerte aller Funktionen stimmen damit überein. Die Standardabweichung beträgt 73,9. Dieser Wert ist bei allen Funktionen gleich, sowie auch alle Differenzensummen (Differenzen zwischen den Zahlen).
Die einzige Auffälligkeit, die bei den vielen Einzeltests bemerkt wurde, ist der vielfache automatische Seed der Funktion spritz_rand(), der damit einhergeht, daß die Sequenz der generierten Zufallszahlen durch jeden Seed geändert wird: Es geht jedesmal eine neue Saat auf. Dies ist zweifellos ein Qualitätsmerkmal, das bewirkt, daß die generierten Zufallszahlen in ihrer Abfolge besonders zufällig und nicht vorhersagbar sind. Der Kern-Algorithmus des Spritz ist dem des Arc4 überlegen.
Wikipedia-Artikel: Arc4 + Spritz
Vorstehend der Seed-Abschnitt der Funktion spritz_rand().
Die Struktur seed erhält den zufälligen Prozeß-ID, die Zeit
in Sekunden und einen großen Teil nichtinitialisierte Zufallsdaten
aus dem Stack-Speicher (buf[]).
Aus dem Array wv[] wird ein von der Sekundenzeit bestimmter Wert gewonnen.
Beide Quellen mit Zufallsdaten verschiedenster Art werden verwendet, um diese
Daten in 256 Schritten in den laufenden Kern-Algorithmus zu impfen.
Danach wird die S-Box des Kern-Algorithmus in 1024 Schritten eingefahren.
Der Count von 1600000 wird an verschiedenen Stellen der Funktion um
jeweils 1··8 reduziert.
Sobald cnt <= 0 ist, wird
ein neuer Seed aufgesucht.

Ich war zweimal live dabei, als diese Ziehungsmaschine (aus Frankreich)
in der Sendung wegen Fehlers stehen blieb, im Beisein des Programmdirektors (o.ähnl.).
Dieses Ziehungsgerät wurde alsbald wegen Unzuverlässigkeit durch ein
anderes Gerät ersetzt, das mit Luftdruck Tischtennisbälle durch den Innenraum
eines transparenten Gefäßes blies.
Das abgebildete Gerät weist zwei gegenläufig rotierende Stabträger auf, mit
drei Stäben auf der inneren Antriebsscheibe und vier Stäben auf dem äußeren Ring.
Diese Stäbe wirbelten die Bälle kräftig durcheinander.
Es ist erkennbar, daß in der Darstellung sich viele Bälle momentan
fliegend im oberen Bereich befinden.
Genau dort verklemmte sich ein Ball zwischen zwei gegenläufig rotierenden Stäben
und versursachte einen Halt der Maschine.
Der Fehler der ansonsten guten Maschine waren temporär zu geringe
herbeirotierte Abstände, die nicht größer als der Balldurchmesser waren.