Phasenerkennung
Puffer für OPV
Gleichrichter mit Sieb-Drossel
Oszillatoren für induktive Näherungsschalter
Oszillator für induktive Näherungsschalter (2)
Multiplikatives Mischen von Sinus-Signalen
Synchronisierter Oszillator
Impedanz am Emitter eines Emitterfolgers
Standby-Schaltung mit nur 7 nA Strom
Notch(Kerb)-Filter mit verstellbarer Güte Q
Regler für Labor-Netzgerät mit Premium-Daten
Basis-Emitter-Kennlinie
Mischen von Sinus-Signalen
Mischen von Sinus-Signalen 2
Mischen von Sinus-Signalen 3 (Gilbert-Zelle)
Spannungs-Begrenzer für Signale
Bessere Crowbar-Alternative - NEU
Schalten mit drei Transistoren
Schalten mit drei Transistoren (2)
Fehlerhafte Spice-Modelle
Fehlerhafte Spice-Modelle (2)
Fehlerhafte Spice-Modelle (3)
15.Jun.2020
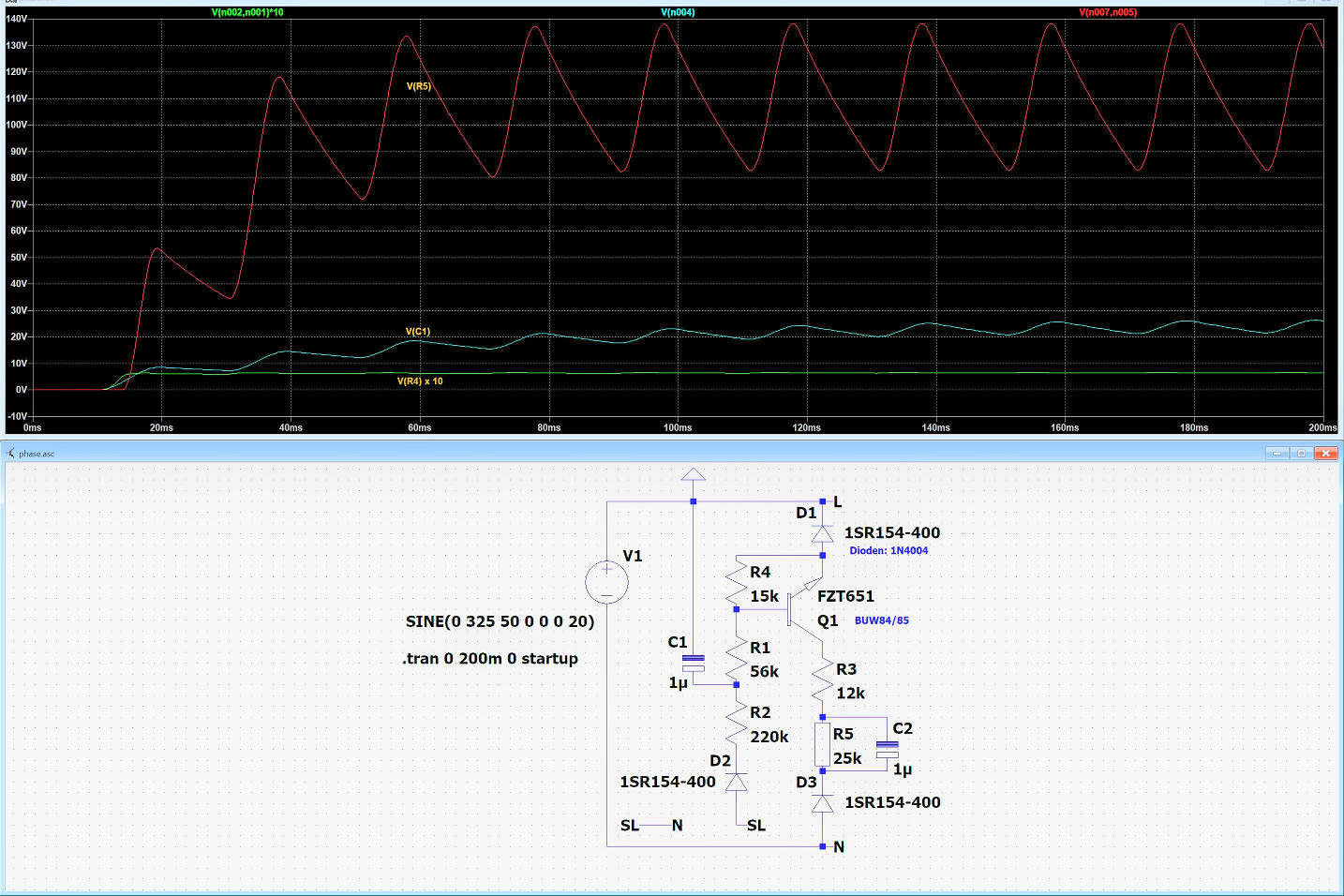
Die vorstehende Schaltung ist für Wechselspannung 230 V~ an Schuko-Steckdosen bestimmt und detektiert, ob am Anschluß L eine Phase anliegt oder nicht. Dazu wird der Schutzleiter SL benutzt, der ja vor einem FI-Schutzschalter mit dem Neutralleiter N und Erdpotential verbunden ist. Wenn also an Anschluß L kein Phasenpotential ist, ist hier Schutzleiterpotential, wodurch praktisch 0 V an der Ansteuerstrecke des Transistors anliegt.
Widerstand R5 stellt den Spulenwiderstand (110 V) eines Relais dar. Dieses Relais schaltet die Phase an L an den Phasenanschluß eines Gerätes, daß bei anderer Polung defekt gehen kann. Ist die Polung falsch, bleibt das Relais unerregt und der Schuko-Stecker muß anders herum eingesteckt werden. Das Relais kann nicht direkt verwendet werden, um mit 2 Wechslern eine automatische Korrektur vorzunehmen, da über Öffner-Kontakte kurzzeitig eine falsche Polung vorliegen kann. Für eine Automatik müssen daher insgesamt 3 Relais verwendet werden.
Widerstand R3 stellt eine geeignete Spannung für R5 ein, und begrenzt den Strom wegen C2. R1 ist erforderlich, um einen genügenden Spannungsabstand (Reserve) für die Basis herzustellen. Es ist im Diagramm erkennbar, daß mit den vorliegenden Bauelement-Werten große Variationen an eben diesen möglich sind. Der Wert von C2 ist allerdings als Mindestwert anzusehen. C2 und R3 sind vom Relais (R5) abhängig. Durch höhere Kapazitäten wird die Schaltung träger. Der Transistor ist nach 20 ms eingeschaltet, nicht jedoch das Relais.
19.Jun.2020
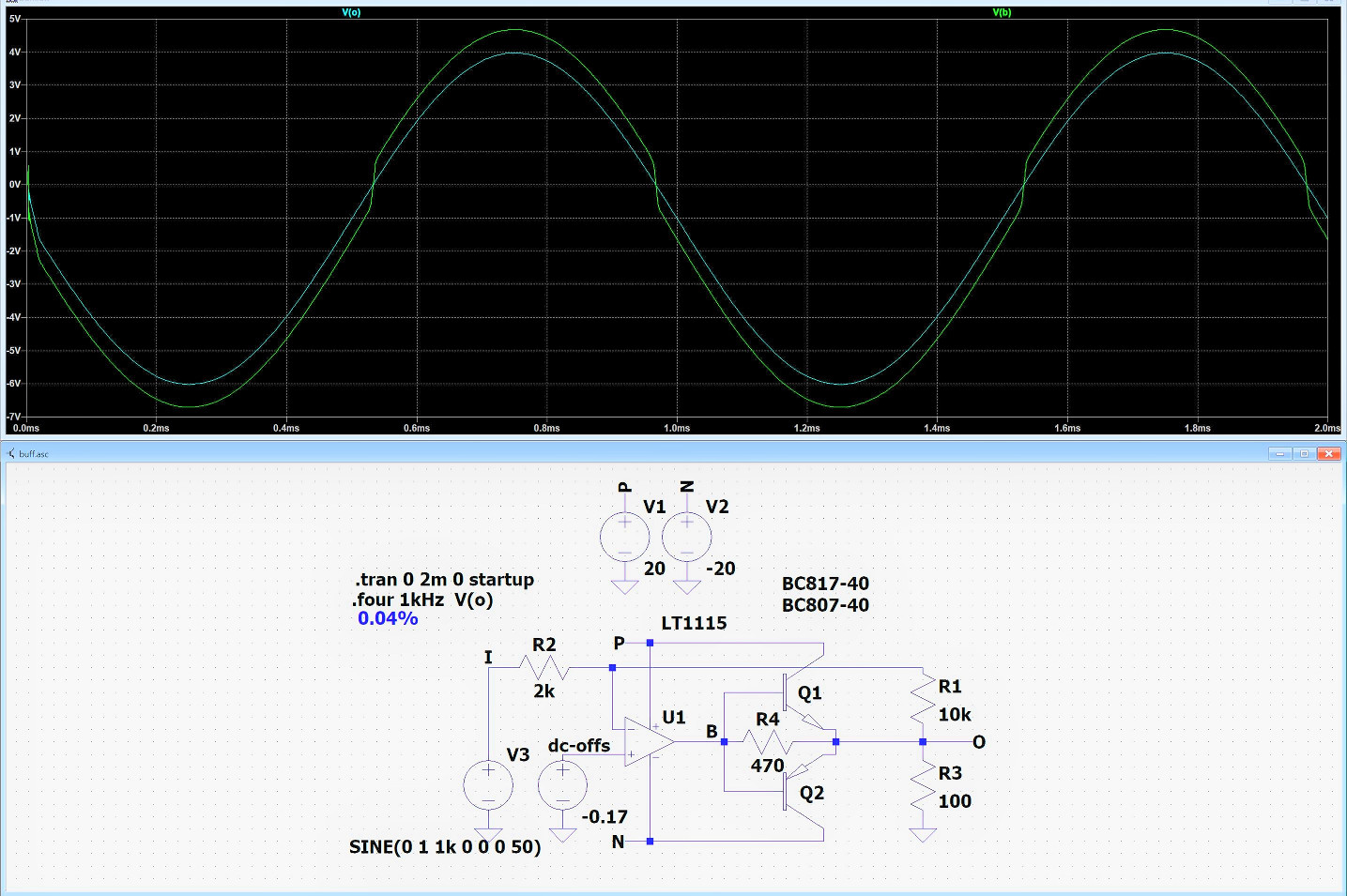
Die vorstehende Schaltung zeigt die einfachste Gegentakt-Pufferstufe für einen Operationsverstärker. Es wurde im Interesse von Einfachheit auf einen Ruhestrom verzichtet. In den meisten Fällen ist eine solche Lösung mehr als ausreichend. Diese Schaltung hat einen Klirrfaktor von 0,04 % bei 1 kHz. Das ist fast immer voll zufriedenstellend. Das Signal (grün) an den parallel geschalteten Basen überschreitet schnell die beiden B-E-Spannungen von insgesamt etwa 1,4 V. Am Plus-Eingang des OPV ist ein Offset von -0,17 V eingestellt. Das ergibt eine Verschiebung der Ausgangsspannung 'O' um -1 V, weil die Verstärkung vom Plus-Eingang aus 6 beträgt (R1/R2+1), wohingegen die Verstärkung für den Eingang 'I' 5 beträgt (R1/R2).
09.Aug.2020
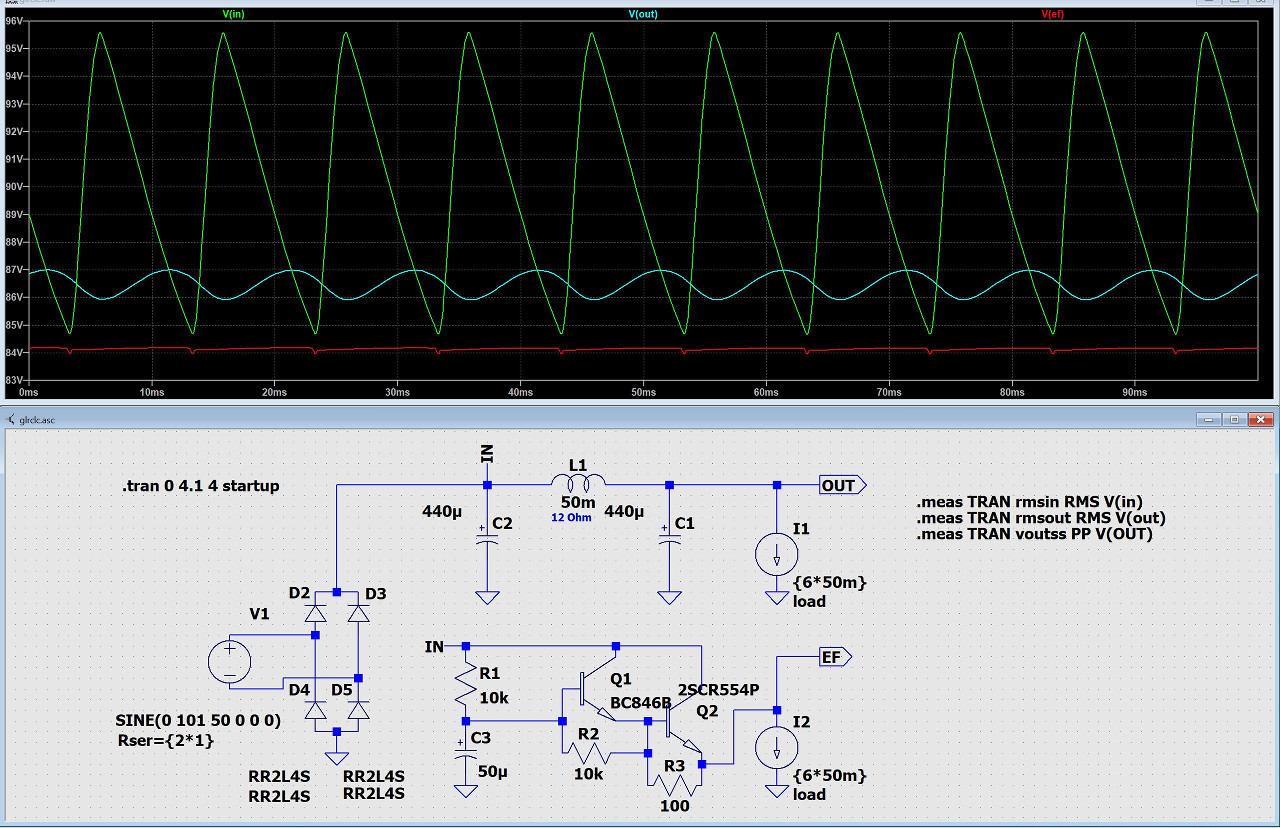
Siebdrosseln waren in den 1960er und 1970er Jahren noch zeitgemäß. Später aber nicht mehr, was hier auch demonstriert wird. Eine wirksame Siebdrossel muß eine recht hohe Induktivität haben. Es ist schwierig, diese Forderung mit einem geringen Kupfer-Widerstand zu kombinieren. Die Brummspannung ändert sich von einer Sägezahn-Form zu einer Sinus-Form durch die Anwendung einer Siebdrossel.
Die Schaltung unten ist ein RC-Glied mit nachfolgendem Darlington-Transistor als Emitterfolger geschaltet (3 Bauelemente). Diese auf einem Halbleiter-Bauelement basierende Schaltung ist der oberen Schaltung mit Elko+Drossel+Elko weit überlegen, wie der Graph der Ausgangsspannung V(ef) zeigt. Sie ist einfach intelligenter. Da Drossel L1 und Elko C1 entfallen, ist sie zudem kleiner, leichter und verursacht geringere Kosten.
25.Jun.2020
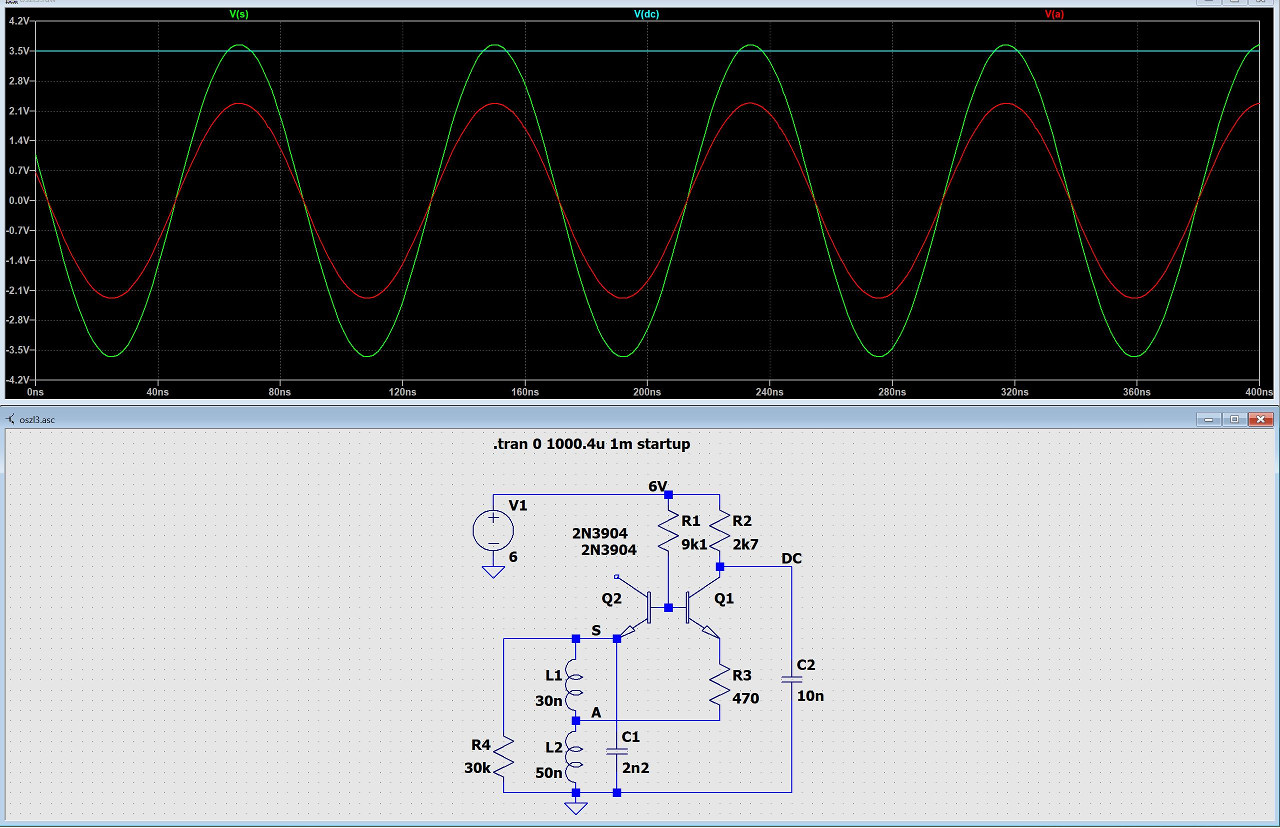
Vorstehende Schaltung ist ein Oszillator mit LC-Schwingkreis. Es handelt sich um einen der einfachsten diskreten Oszillatoren für Induktive Näherungsschalter. In solchen Geräten bestehen die Induktivitäten aus einer Wicklung HF-Litze mit Anzapfung (A) in einer Hälfte eines Ferrit-Schalenkerns, womit auch eine magnetische Kopplung besteht.
Die Induktivitäten L1 und L2 in der LTspice-Simulation bilden gemeinsam mit C1 einen Transformator, der vom Emitterfolger Q1 gespeist wird, der ja ohne Transformator eine Spannungsverstärkung von < 1 hat und damit nicht schwingen kann. Die Spannungen V(a) und V(s) zeigen die transformatorische Wirkung. Die Induktivitäten im realen Ferrit-Kern haben auch eine magnetische Kopplung über den Ferrit-Kern.
V(dc) ist eine Gleichspannung, die zu einem Schmitt-Trigger geführt werden kann, der ein digitales EIN/AUS produziert und eine genügend große Hysterese in Anbetracht der Wirkung von C2 haben muß. V(dc) bewegt sich in Abhängigkeit der Dämpfung des Schwingkreises. Diese Dämpfung bewirkt Widerstand R4, der für eine Dämpfung durch ein Metall in der Nähe der Ferrit-Spule steht. Mit R3 kann der Schaltabstand des Näherungsschalters eingestellt werden. C1 muß die Keramik-Art NP0/C0G haben.
Zwischen den Emittern von Q1 und Q2 muß die Gleichspannung 0 V sein.
Andernfalls wird der Schwingkreis stark bedämpft, so daß der Oszillator
nicht anschwingt.
Deshalb ist anstelle von Q2:B-E auch keine einzelne Diode eingesetzt.
Der Oszillator erreicht regelmäßig eine Frequenz der
Periode bedämpft/unbedämpft von 5 kHz.
Der Näherungsschalter hat eben ungefähr diese maximale Schaltfrequenz.
Dieser Oszillator wurde auch mit einer Schwingfrequenz von 55 MHz
konkret aufgebaut – natürlich ganz anders dimensioniert
(Silberdraht-Spule, etc.).
Dieser Oszillator ist gut störfest.
Andernfalls wäre er nicht für Näherungsschalter in der Industrie geeignet.
30.Jun.2020
^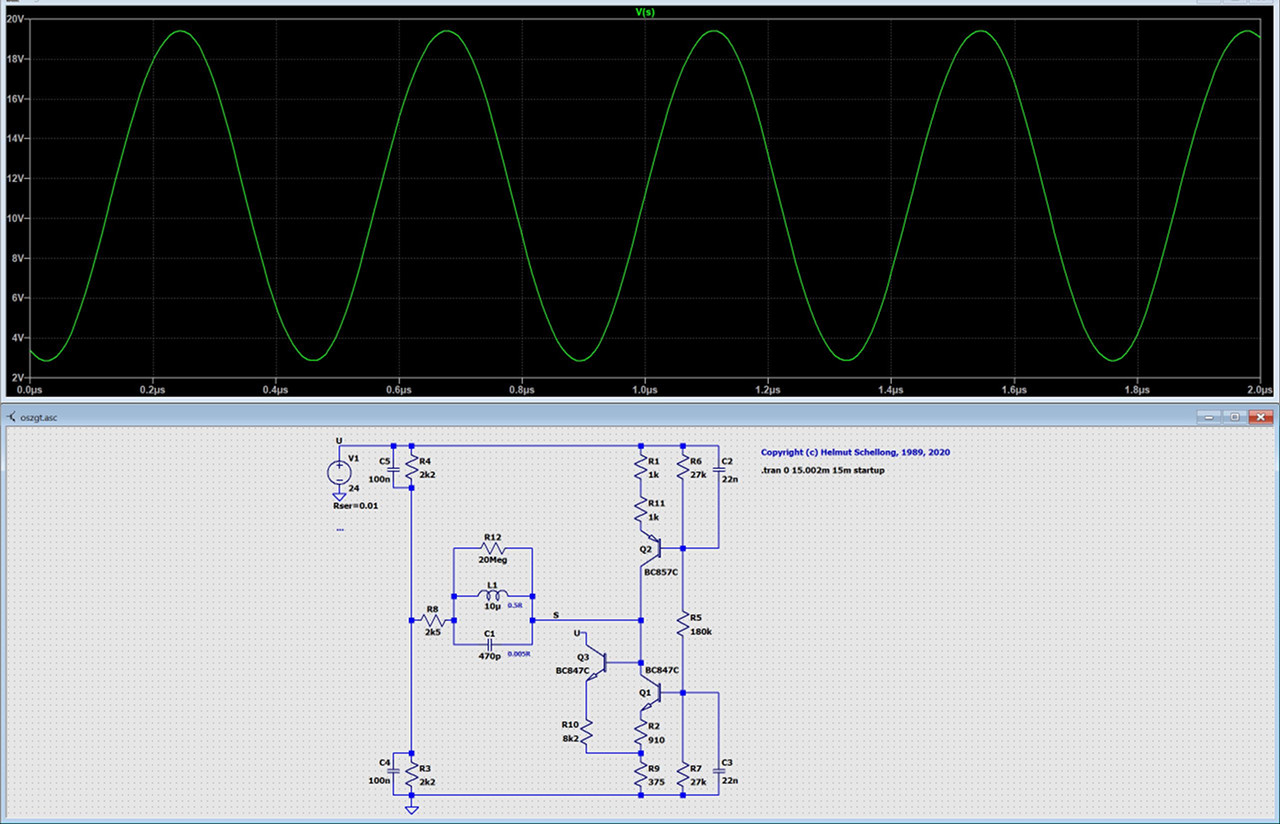
Die vorstehende Schaltung ist ebenfalls ein Oszillator für Induktive Näherungsschalter. Zusätzlich ist eine Eignung für Metallsuchgeräte vorhanden. Die Schaltung ist ein Entwicklungsmuster, also kein Bestandteil eines industriellen Serienproduktes. Die Schaltung hätte zur Patentanmeldung angeboten werden können.
Dieser Oszillator hat eine extrem hohe Sensitivität. Beim anderen Oszillator weiter oben bewirkt der bedämpfende Widerstand mit 100 kΩ keine merkliche Dämpfung. Bei diesem Oszillator ist R12 mit 20 MΩ gerade eben außerhalb einer sichtbaren Bedämpfung.
Die Schaltung wurde 1989 mit einem halben Ferrit-Schalenkern 9 mm ∅ getestet. Der Standard-Schaltabstand beträgt hier 4 mm nicht-bündig. Mit diesem Oszillator konnte im Labor ein maximaler Wirkabstand von 25 mm erreicht werden. Das ist für den verwendeten Schalenkern-Durchmesser ein extrem hoher Wert. Die Schwingkreis-Induktivität benötigt hier keine Anzapfung, kommt also mit zwei Anschlüssen aus.
04.Aug.2022
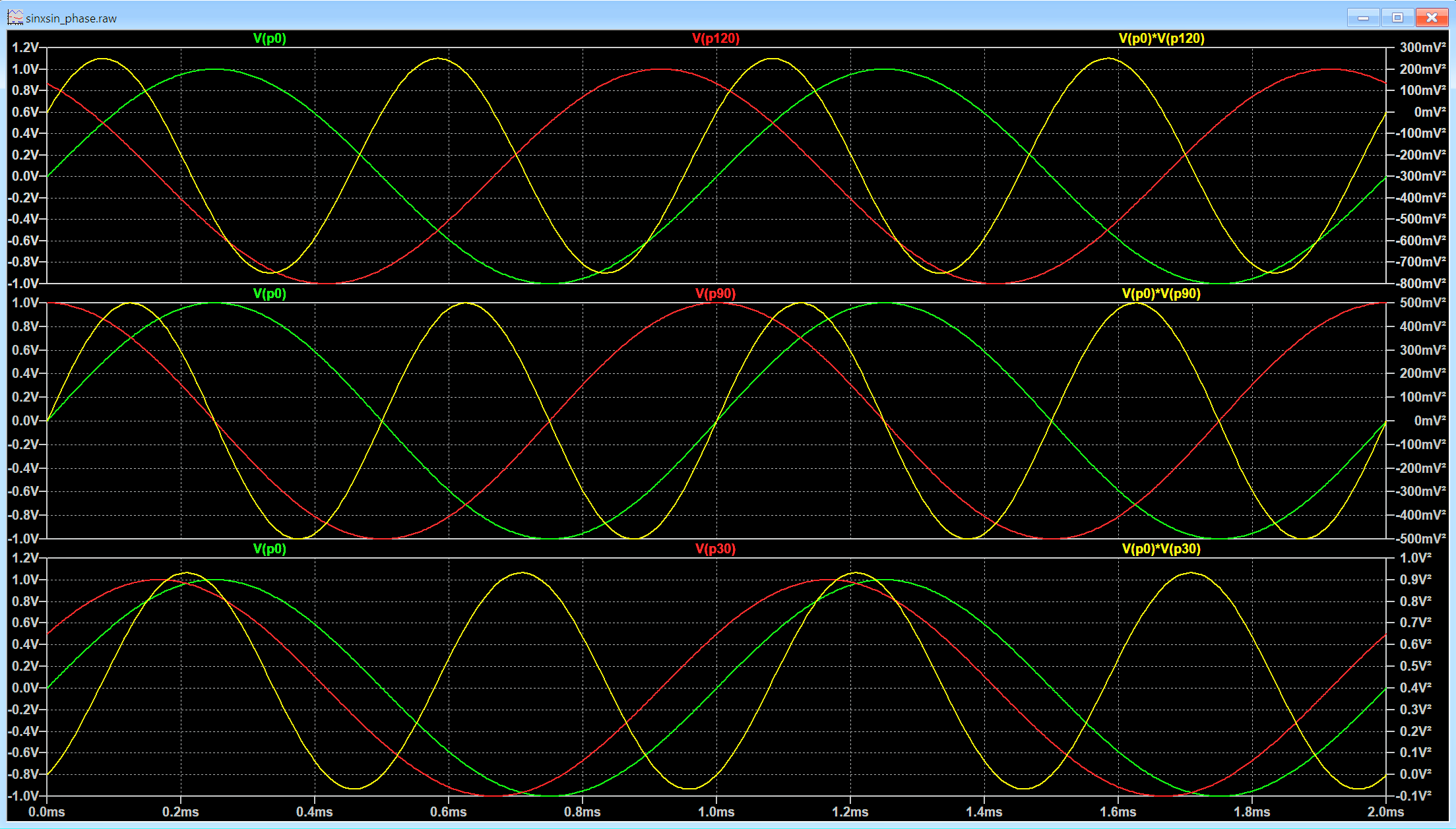
Vorstehend werden je zwei Sinus-Signale grün und rot mit gleicher Frequenz multiplikativ verknüpft (gelb). Die Phasenverschiebungen zwischen grün und rot betragen 120, 90 und 30 Grad. In allen Fällen hat die resultierende Mischspannung (gelb) die doppelte Frequenz (f1+f2). Bei 90° ist die Mischspannung symmetrisch um die 0-Linie herum. Bei 120° hat die Mischspannung einen negativen DC-Offset, bei 30° einen positiven DC-Offset. Die vertikalen Skalen rechts zeigen dies.
08.Aug.2022
Siehe auch vorstehendes Dreifach-Diagramm.
Leicht unterschiedliche Frequenzen (frei laufend):


Die Grundfrequenz frei laufend beträgt 947 kHz, die Sync-Frequenz 955 kHz. Für die Hüllkurve wurde die Sync-Frequenz auf 975 kHz erhöht, damit mehr als eine Periode der Hüllkurve sichtbar ist. Bei gleichen Frequenzen ist die Frequenz der Hüllkurve = 0, deren Amplitude ebenso.
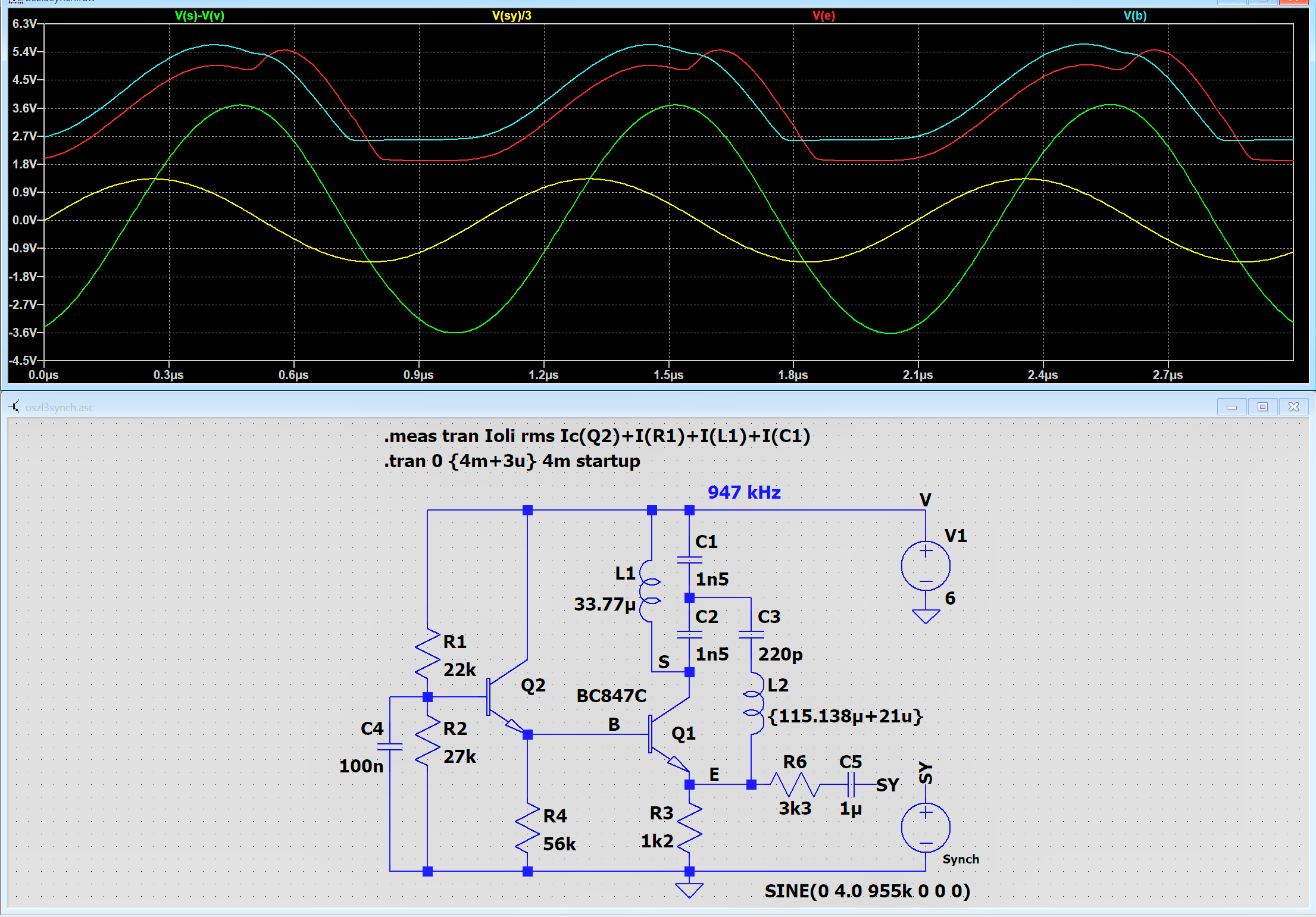
Der Oszillator (grün) befindet sich im synchronisierten Zustand.
Die Sync-Spannung (gelb) wurde im Diagramm reduziert.
Eine multiplikative Mischung wird hier durch die nichtlinearen Kennlinien
(BE-Strecke) der Transistoren verursacht.
Der Oszillator ist nicht minimal, sondern vielseitig ausgestattet.
Es sind ein Parallel- und ein Reihen-Schwingkreis vorhanden.
Die Induktivität im Reihen-Schwingkreis darf entfallen.
Der Kondensator kann dann direkt mit dem Kollektor verbunden werden.
Es muß in diesem Fall nur ein Kondensator im Parallel-Schwingkreis vorhanden sein.
Die beiden Kondensatoren im Parallel-Schwingkreis mit Mittelanzapfung
verbessern Einstellbereiche merkbar bei Verwendung von Reihen-Schwingkreis
oder Quarz anstelle des Reihen-Schwingkreises.
Der Zieh-Trimmkondensator eines Quarzes sollte üblicherweise einen Wert von
5..50 pF haben, nicht den hier sichtbaren hohen Wert.
Die Werte der Induktivitäten mit Nachkommastellen wurden mittels der Formel
L = 1 ⁄ [ C (2πf)² ] für
f = 1000 kHz berechnet.
f = 1 ⁄ [ 2πf √LC ]
Durch die Verbindung beider Schwingkreise miteinander passiert eine Verstimmung, die
durch die Addition beim Wert für L2 ausgeglichen wurde.
Beide Transistoren arbeiten in Basis-Schaltung.
Das bedeutet, daß jeweils eine sehr geringe AC-Impedanz
(z.B. idealisiert 0 Ω)
zwischen Basis und GND vorliegen muß.
Der Widerstand R4 hat eine sehr große Wirkung (wohl oft unvermutet).
Er kann prinzipiell entfallen, wodurch allerdings bei manchen Variationen der Schaltung
ein Anschwingen unterbleibt.
Durch den Wert von R4 wird derjenige Teil der Kennlinie bestimmt, in dem Transistor Q2 arbeitet.
Dadurch verändert sich ziemlich linear und über einen großen Bereich die Impedanz am Emitter
und damit die Impedanz für die Basis von Q1.
Bei ungefähr 10 kΩ ist die Schwingkreis-Spannung (S) zu groß
und stark verzerrt (Clipping).
R4 kann praktisch bis hinab auf den ungefähren Wert von R3 reduziert werden.
Zu größeren Werten hin wird der Oszillator zusehends weicher in seinem Verhalten.
Beispielsweise sinkt die Amplitude der Schwingung deutlich.
Die Verzerrungen sinken ebenfalls.
Eine Einspeisung des Sync-Signals an der Basis von Q2 funktioniert zwar
(ideal zwischen C4 und GND).
Allerdings ergibt sich ein deutlich größerer Einstellbereich bei Einspeisung
am Emitter von Q1.
Dort wird wiederum wesentlich mehr Signal-Leistung benötigt, und
die Ankopplung an den Emitter ist wesentlich beeinflussender
und insgesamt problematischer.
Beispielsweise gibt es zwischen den Werten 1µ und 220n für C5
erkennbare Unterschiede bei der Schwingung S und bei V(b), obwohl der
Blindwiderstand Xc für 220n nur etwa 0,7 Ω beträgt.
Es muß eine Entscheidung getroffen werden, ob die Sync-Spannung ständig verbunden
oder steckbar/schaltbar sein soll. Bei permanenter Verbindung kann die
Spannung ja den Wert 0 annehmen, was die Spannung ebenso außer Wirkung setzt.
Der Ziehbereich ist abhängig von der Höhe der Sync-Spannung.
Das Verhältnis von L und C im Schwingkreis ist hier auch bedeutsam.
Ein regelrechtes Einrasten auf 90° wie bei einer PLL findet nicht statt.
Die Wörter Fangbereich, Herausfallen und Ausrasten sind unpassend.
Das Verhalten enthält keinen Hysterese-Effekt, wie bei magnetischen Kanten
im Grafik-Bereich.
Die Sync-Spannung kann prinzipiell an allen Steuer-Elektroden eines Transistors
angelegt werden, mehr oder weniger direkt.
Eine wichtige Anwendung ist es, einen Oszillator wahlweise über einen Steck-Anschluß
mit der wesentlich höheren Frequenzstabilität des Signals einer
externen Referenz zu synchronisieren.
10.Aug.2022
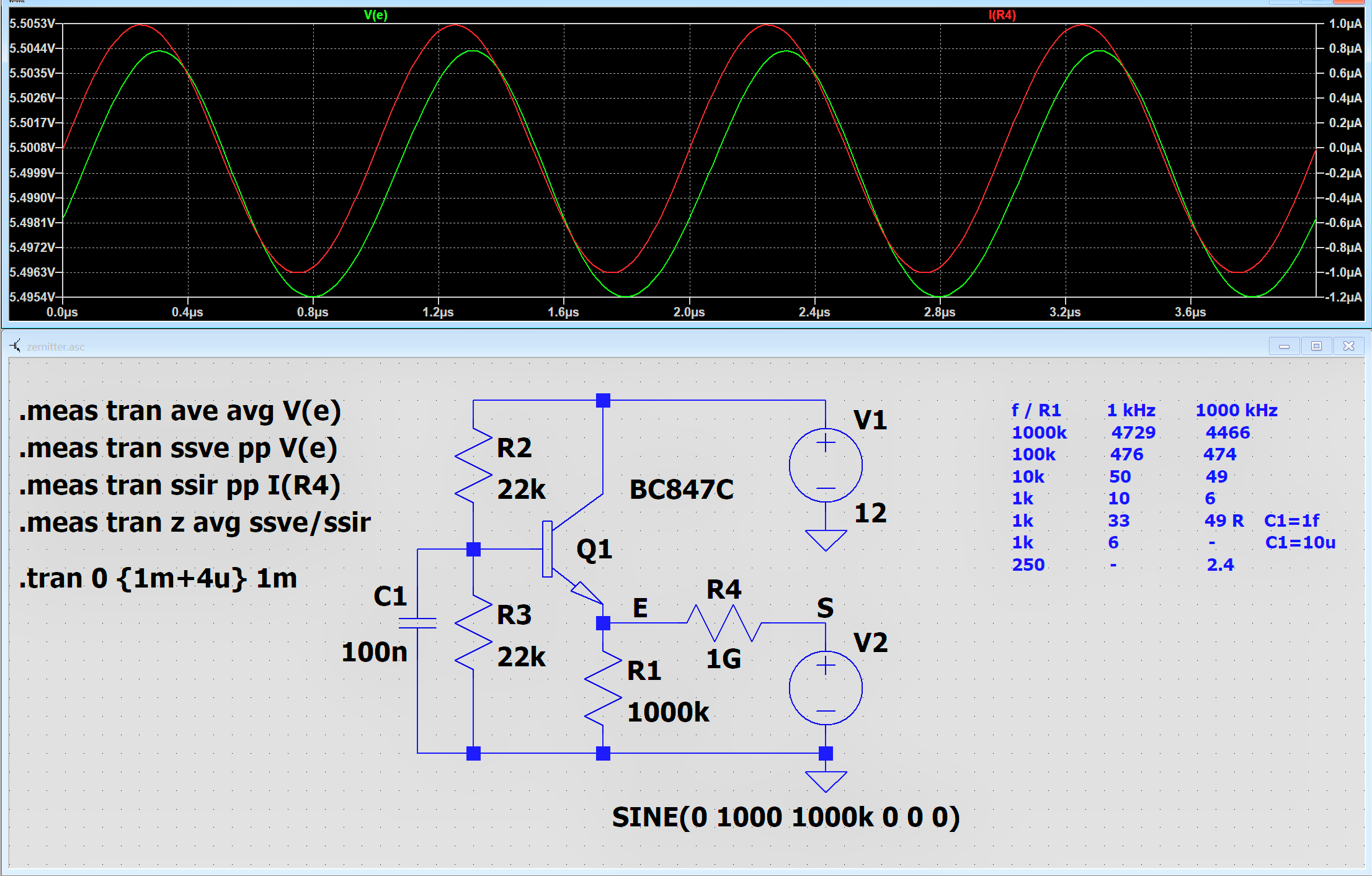
Die Impedanz Z am Emitter wird im Error-Log (Ctrl-L) abgelegt.
Gemessen wurde mit 1000 V Spannung und extrem hohem Widerstandswert.
Das bewirkt eine Quasi-Stromquelle.
Eine Tabelle mit den Impedanzwerten in Ω ist direkt neben der Schaltung
als Text angegeben.
Die Phasenverschiebung im Diagramm wird durch kleine parasitäre Werte bewirkt, im
Zusammenhang mit den großen Widerstandswerten und 1000 kHz Arbeitsfrequenz.
Der Kondensator C1 wirkt unübersehbar besonders bei 1000 kHz.
Wird er entfernt (C1=1fF), steigt die Impedanz am Emitter sehr beträchtlich.
Bei 1 kHz ist eine minimale Impedanz ebenfalls erreichbar, wenn C1
entsprechend angepaßt wird.
Der Wert von R1 bestimmt, in welchem Teil seiner Kennlinie Q1 arbeitet.
Die Kennlinie wird steiler, je höher der Strom ist.
Beim analytischen Betrachten der Wertetabelle fällt auf, daß das Verhältnis
zwischen R1 und Impedanz ziemlich genau 200 beträgt.
Erst bei den geringsten Werten der Impedanz ist erkennbar, daß das Verhältnis
beginnt, andere Werte anzunehmen. Die Kennlinie wird nicht mehr steiler.
Bei anderen Schaltungen kann folglich nach Feststellung dieses Verhältnisses
(beispielsweise mit R1 = 10k) das festgestellte Verhältnis
dazu verwendet werden, die restlichen Impedanzwerte zu berechnen.
Beim Oszillator wird von der einstellbaren Impedanz
des Emitters Q2 ausdrücklich Gebrauch gemacht.
29.Jul.2020
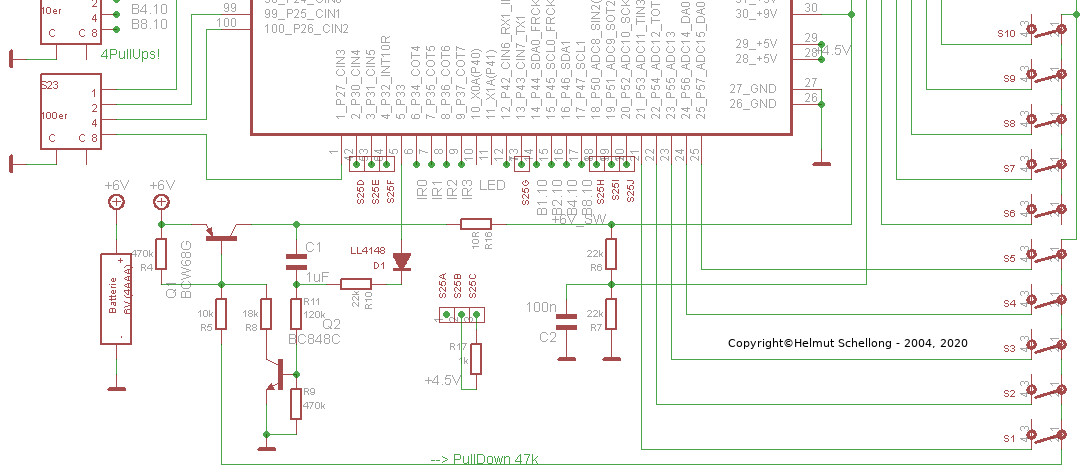
Vorstehend eine Schaltung für einen Mikrokontroller, die im Standby-Modus die versorgende Batterie (6V) mit nur 7 nA Strom belastet. Im Aktiv-Modus beträgt der Strom durch den Transistor Q1 typisch 55 mA. An dem Transistor fallen dann etwa 30 mV ab. An R16 (10R) fallen 0,55 V ab, so daß der Mikrokontroller mit etwa 5,4 V versorgt wird.
Wird eine Taste (Sx, rechts) betätigt, wird an R5 (10k) ein PullDown mit 47 k geschaltet. Transistor Q1 wird durchgeschaltet. Kondensator C1 bewirkt über Transistor Q2 eine zeitweise Selbsthaltung (Mitkopplung) von Q1. Die Selbsthaltung wird alsbald durch die Software im Mikrokontroller mittels D1 und R10 übernommen. An C1 stellt sich längerfristig eine Spannung von ungefähr 1,5 V ein.
Wenn die Software die Spannung an D1 abschaltet, lädt sich C1 über R11 weiter bis auf etwa 5,3 V auf, bis Q2 nicht mehr genügend Basisstrom erhält, so daß in Folge auch Q1 über R8 nicht mehr im durchgeschalteten Zustand bleibt. Die Spannung am Kollektor des Q1 und damit am plusseitigen Anschluß von C1 fällt gegen Null, getrieben durch den Mikrokontroller als Lastwiderstand von etwa 100 Ohm, wodurch C1 erneut eine Mitkopplung erzeugt, die eine negative Spannung an der Basis des Q2 bewirkt. Dies sperrt Q1 beschleunigt. Anschließend entlädt sich C1 vollständig, da an seinen beiden Anschlüssen Widerstandspfade nach Masse vorhanden sind.
Der Strom 7 nA ist einfach der tatsächliche (gemessene) Sperrstrom des Q1, der laut Datenblatt maximal 20 nA betragen kann.
20.Okt.2020
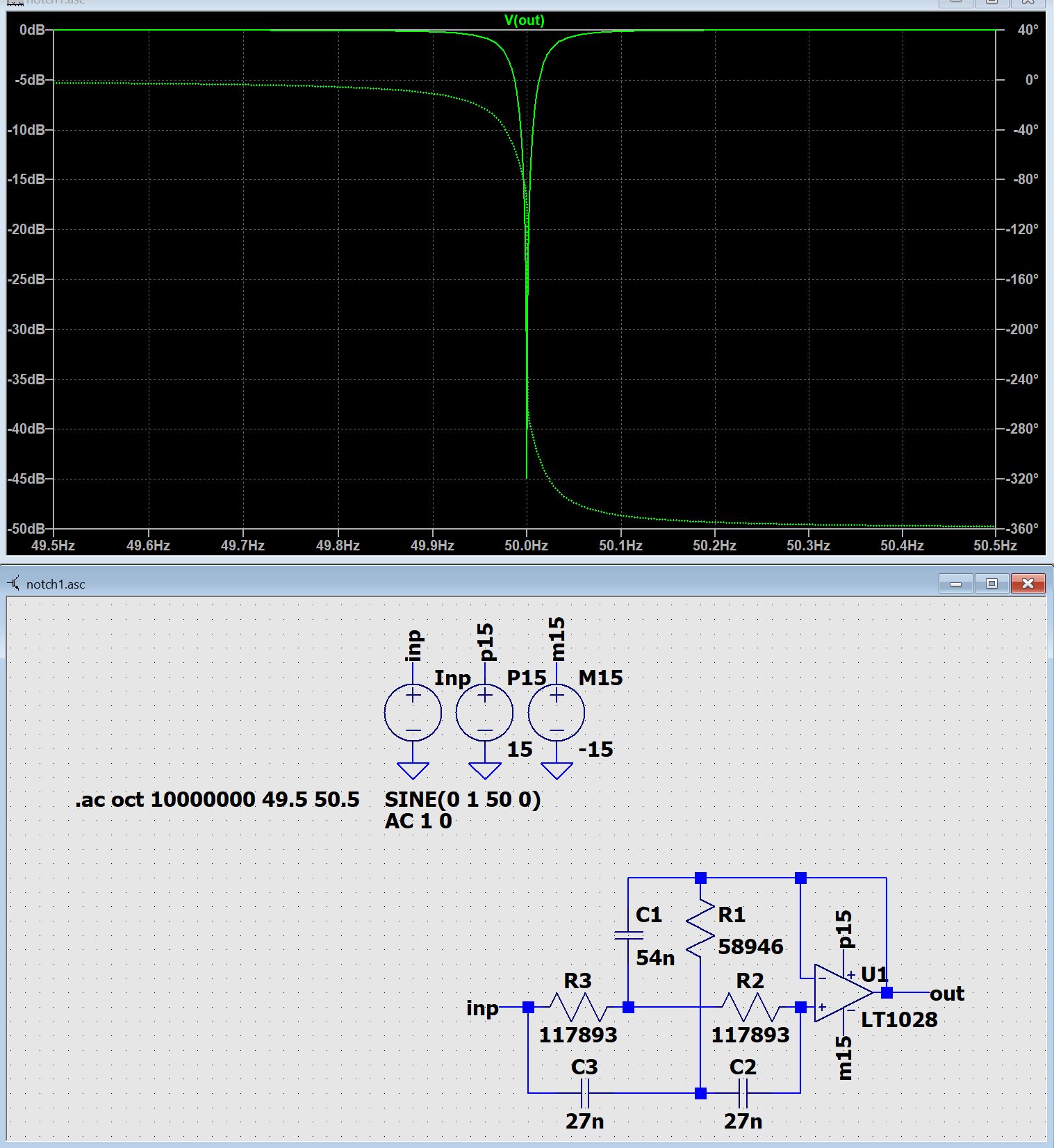
Die Werte der Bauelemente müssen extrem genau eingehalten werden.
Mindestens auf 0,1 % genau.
Dies gilt für R2 = R3 = 2 R1
und C2 = C3 = C1 ⁄ 2.
Die Formel f = 1 ⁄ (2π R C)
ist unabhängig von den vorstehenden Formeln.
Hier einsetzbar sind R2 oder R3 und C2 oder C3.
Voreingestellt für das Filter sind f = 50 Hz.
Es muß ein wirklich guter OPV verwendet werden. Andernfalls ist die Kurvenform stark unsymmetrisch und die Dämpfung sehr gering. Keramische Kondensatoren müssen von der Art NP0/C0G sein, oder SiCap. Folien-Kondensatoren sollten von der Art Polypropylen (PP) 63V- sein. Widerstände sollten vom Typ MELF Metallschicht sein, oder besser.
Die Schaltung im Bild oben hat maximalen Bootstrap-Effekt mit daraus folgender
maximaler Güte (Q).
Die Bauelemente C1 und R1 können anstatt mit dem Ausgang
mit Bezugspotential (Masse; 0V) verbunden werden.
Die Güte ist dadurch minimal.
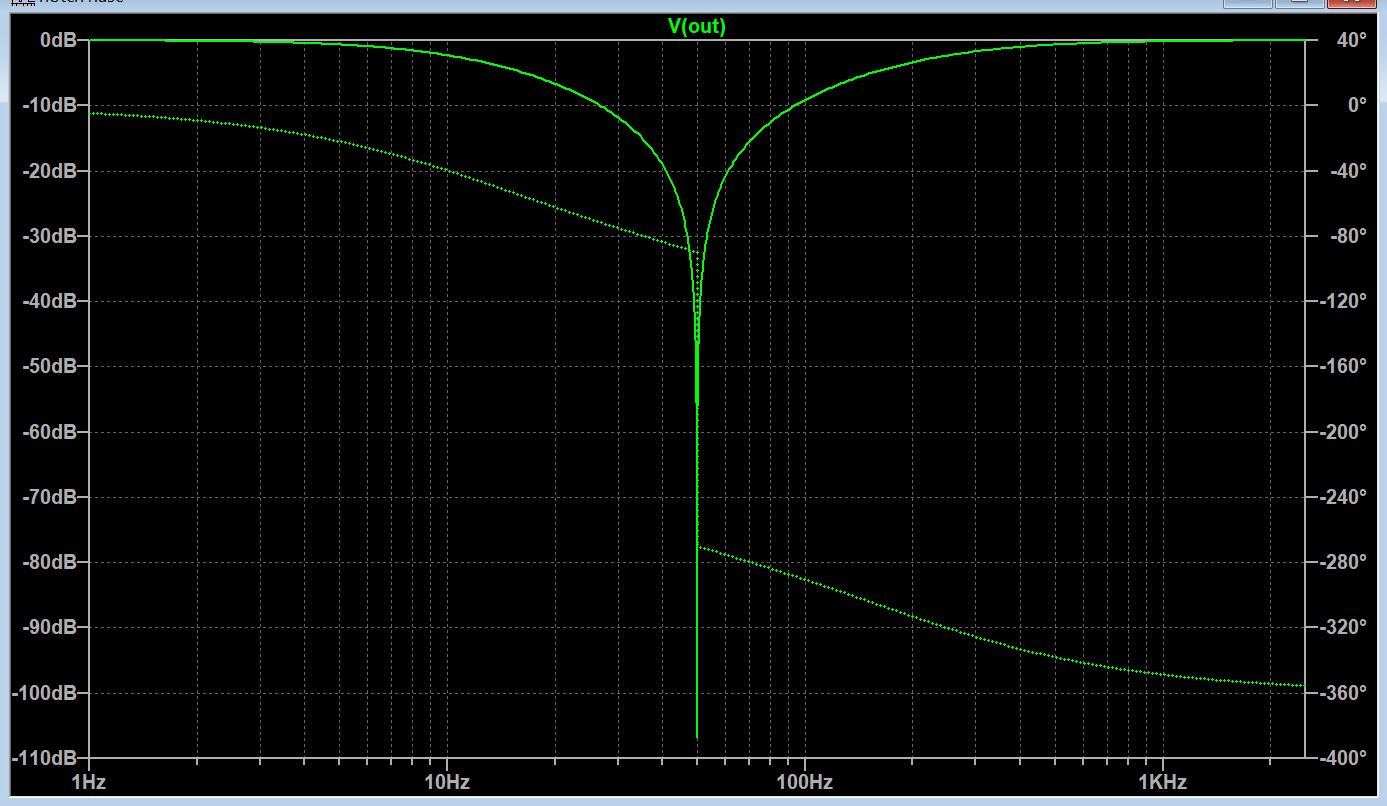
Das erste Kurvendiagramm zeigt dies.
Die Schaltung ist dann kein aktives Filter mehr, sondern ein
passives Doppel-T mit gepuffertem Ausgang.
Zu beachten sind der viel größere Frequenzbereich von 1 Hz bis 2500 Hz
und die Dämpfung von etwa 107 dB.
Die Güte kann stufenlos eingestellt werden, mit einem Trimmer
vom Ausgang nach Masse, Abgriff auf den Eingang eines Puffers, der
eine Verstärkung von 1 hat und dessen Ausgang mit C1 und R1 verbunden ist.
Je geringer die Güte, desto toleranter ist die Schaltung gegenüber Toleranzen bei den Bauelementen. Bei maximaler Güte bewirkt eine Veränderung von C1 von 54,0 nF auf 54,1 nF das Umschlagen auf ein gänzlich anderes Verhalten der Schaltung! Bei 54,01 nF ist zwar kein Umschlagen zu beobachten, jedoch eine sehr wesentlich geringere Dämpfung, und natürlich eine Abweichung von der Soll-Frequenz.
Die Einstellung der Werte der Bauelemente muß mittels (Selektierung und)
Trimmern vorgenommen werden.
Trimmer gibt es für Widerstände und Kondensatoren.
Der Wert eines ohmschen Trimmers in Reihe ist sehr viel geringer als der Wert
des gesamten Widerstandes in Reihe.
Entsprechend fein ist die Einstellung und gering der Einfluß des Trimmers
auf den Gesamtwiderstand, hinsichtlich Temperaturgang und Alterung.
Die Alterung der Bauelemente ist insgesamt vernachlässigbar,
da die Bauelemente keine wirksame Eigenerwärmung haben.
Es werden z.B. vier Widerstände gleicher Art und mit gleichem Wert verwendet.
Zwei davon sind parallel geschaltet für den halben Wert.
Diese werden gleichmäßig und äußerst geringfügig altern.
Die Werte untereinander bleiben folglich im genau gleichen Verhältnis.
Für vier Kondensatoren gilt das ebenso, mit der Ausnahme, daß Parallelität
den doppelten Wert ergibt.
Nach merklicher Frequenzverschiebung durch Alterung wider Erwarten, kann
entsprechend neu kalibriert werden. Die Trimmer sind ja dafür vorhanden.
Dem Temperaturgang kann entgegengewirkt werden, indem die Bauelemente
eng aneinander plaziert werden und Wärmequellen darum herum in geringer
Entfernung vermieden werden.
Es geht hier erneut um die R und die C jeweils untereinander, aber
auch um die beiden Gruppen R und C untereinander.
Der OPV kann bereits eine relevant störende Wärmequelle sein.
Besonders Temperaturgänge können durch viele verschiedene Methoden gemindert werden.
Beispielsweise, indem sich die Temperaturgänge der Gruppen R und C gegenseitig
(teilweise) aufheben.
Das Produkt R × C muß (angestrebt) gleich bleiben.
Bauelemente mit absichtlichem Temperaturgang (PTC, NTC, KTY) können hinzugefügt
werden. Auch mit Widerständen parallel, um deren Wirkung beliebig zu reduzieren.
Und vieles mehr.
Um Frequenzverschiebungen zu beseitigen, muß nur eine Gruppe R oder C
entsprechend kalibriert werden.
Siehe oben die Formel f.
Sollte die zu dämpfende Frequenz zu stark schwanken, kann durch Reduzierung
der Güte die Kerbe im Frequenzgang verbreitert werden.
Beispielsweise die Netzfrequenz schwankt um maximal ±0,2 Hz.
Eine solche maximale Abweichung kommt außerordentlich selten vor.
Die weitaus meiste Zeit weicht die Netzfrequenz nur um ±0,02 Hz ab.
2.Dez.2020
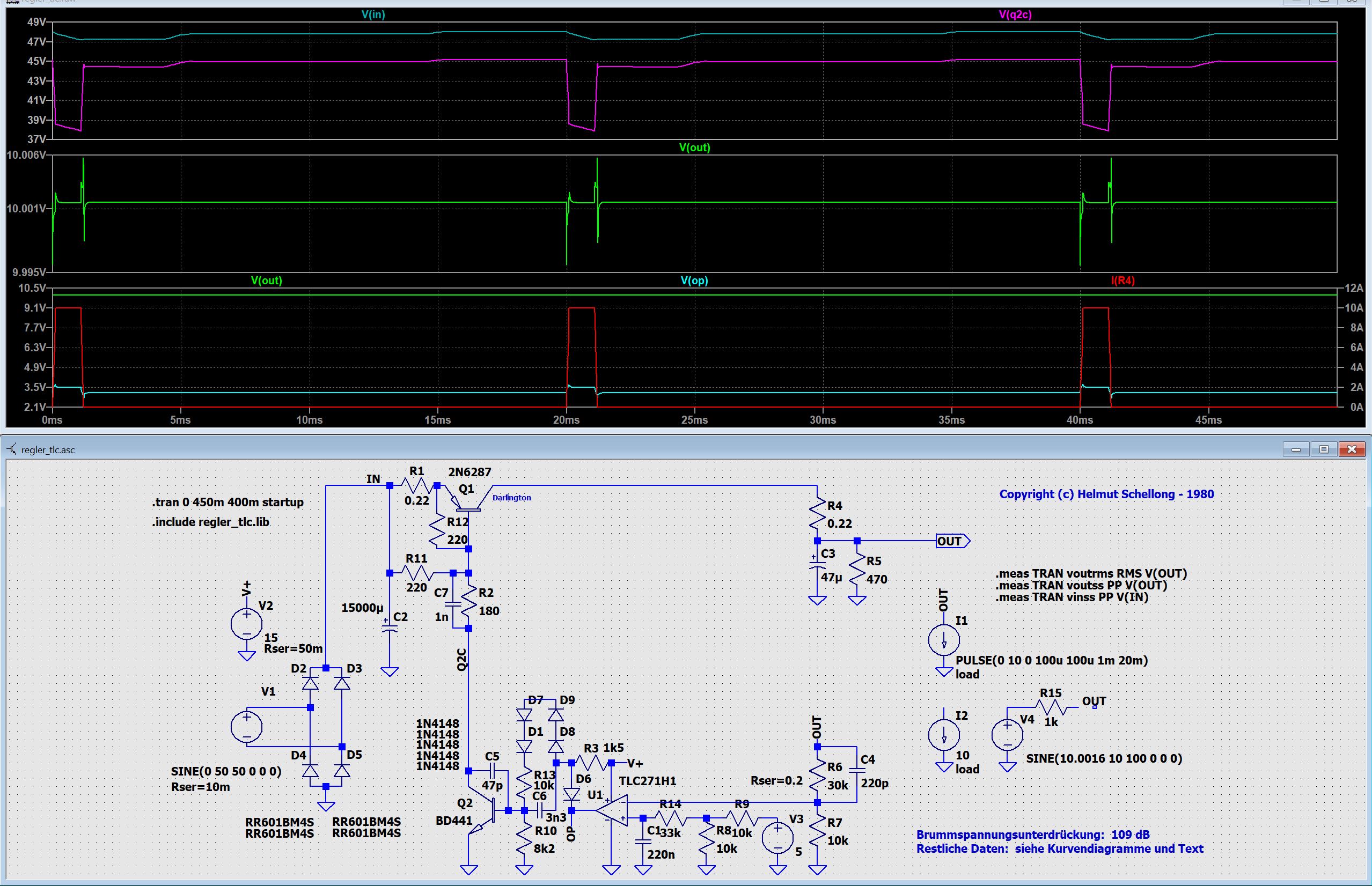
Der vorstehende Spannungsregler stammt aus dem in diesem Foto oben links sichtbaren Labor-Netzgerät, das 1980 entwickelt und gebaut wurde. Die technischen Daten sind extrem gut - ganz außergewöhnlich. Entsprechend anspruchsvoll ist die Schaltung, die einen PD-Regelkreis enthält. Die im realen Gerät vorhandene Stromregelung ist hier nicht dargestellt.
V3 ist im Original eine Referenzdiode LM336-5. Im Original sind BD679 (Darlington) und TIP146 statt BD441 und 2N6287 verwendet. Der Operationsverstärker TLC271 kann seinen Ausgang bis 0 V bringen, und seine Eingänge können bis 0,2 V unterhalb von V- betrieben werden. Für V+ gelten diese Eigenschaften nicht! Der TLC271 wird im Modus High-Bias betrieben - deshalb TLC271H.
Die Simulation verhält sich genau so wie der reale Spannungsregler. Unterschiede sind vernachlässigbar. Das liegt daran, daß bis auf Widerstände und keramische Kondensatoren Modelle verwendet werden. Der in der Simulation eingestellte Strom beträgt 10 A. Im Original wurde nur 1 A eingestellt, um Daten zu ermitteln.
| Aktuell | 1980 | ||||
|---|---|---|---|---|---|
| Parameter | Bedingungen | Frequenz | Wert | Wert | Bedingungen |
| Lastausregelung (Laststrom-Puls 0 A / 10 A) |
Rise time 100 µs | – | ∼6 mV | ∼6 mV | 0 A / 1 A |
| Rise time 1 µs | – | ∼7 µs | ∼5 µs | 0 A / 1 A | |
| Änderung Ausgangsspannung |
Ausgangsstrom 0 A → 10 A |
– | 0,0000 V | – | – |
| Eingangsspannung 100 % → 60 % |
– | -0,0001 V | – | – | |
| Brummspannungsunterdrückung | Laststrom 10 A | 100 Hz | 109 dB | 97..100 dB | Laststrom 1 A |
| Dynamischer Ausgangswiderstand |
Spannungsquelle V4 R15 |
100 Hz | 0,095 mΩ | 0,2 mΩ | 200 Hz |
| 1 kHz | 0,7 mΩ | – | – | ||
| 10 kHz | 17 mΩ | – | – | ||
| 100 kHz | 50 mΩ | – | – | ||
| Allgemein gültig | Ausgangsspannung 10 V Ausgangsstrom 10 A |
Ausgangsstrom 1 A | |||
Diese Daten sind extrem gut!
Insbesondere, wenn der relativ geringe Aufwand und die geringen Kosten
berücksichtigt werden.
Die realen Meßergebnisse:
Daten 1980.
Im Bild in der Ecke links unten.
Die 1980 an realer Hardware festgestellten Daten sind den aktuellen,
durch Simulation generierten Daten, sehr ähnlich.
Die alten Daten wurden mit Oszilloskop Hameg 512N gemessen.
Deshalb sind die Lastausregelzeiten (4/5 µs) auch besser.
Nämlich weil eine anhängende geringe Welligkeit nicht sichtbar war, die
in der Simulation durch Aufzoomen erkennbar wurde.
Eine Steigerung des Laststroms verändert übrigens viele Daten kaum.
Im Regelfall müssen Bauteile, durch die der Laststrom fließt, angepaßt
werden - mehr nicht. Der Regelkreis ist ja fast vollkommen unabhängig
vom Laststrom - weil schließlich die Spannung geregelt wird.
16.Aug.2022
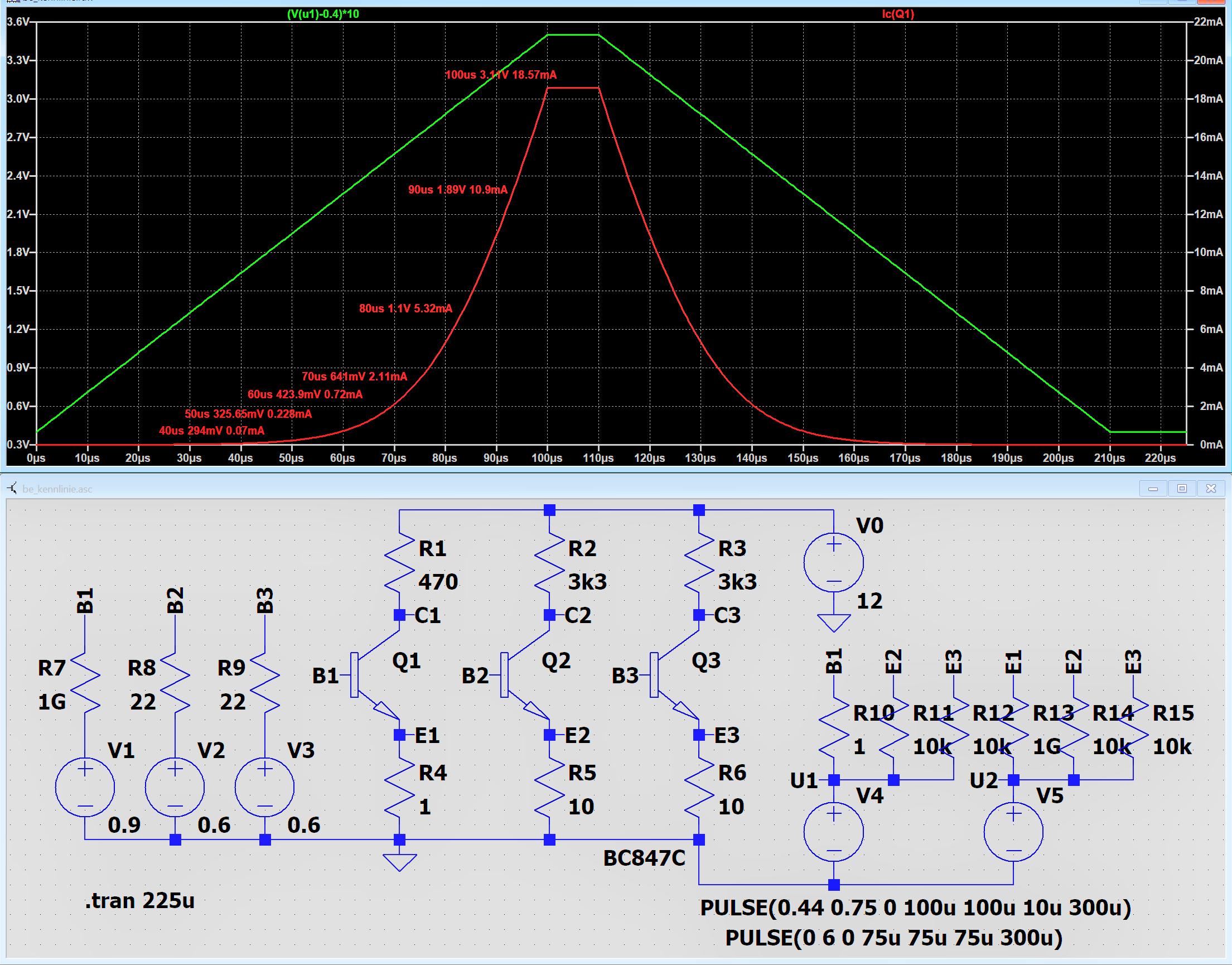
Im vorstehenden Bild wurde nur der Transistor Q1 konfiguriert und dessen Kurven im Diagramm dargestellt.
Die Titelleiste des Diagramms zeigt die Darstellungsfunktionen.
Links und rechts die Skalen für BE-Spannung und Kollektor-Strom.
Die Spannung ist skaliert, weshalb die wirkliche BE-Spannung
mittels der Formel V(u1) = V⁄10+0.4 errechnet
werden muß, falls Bedarf vorliegt.
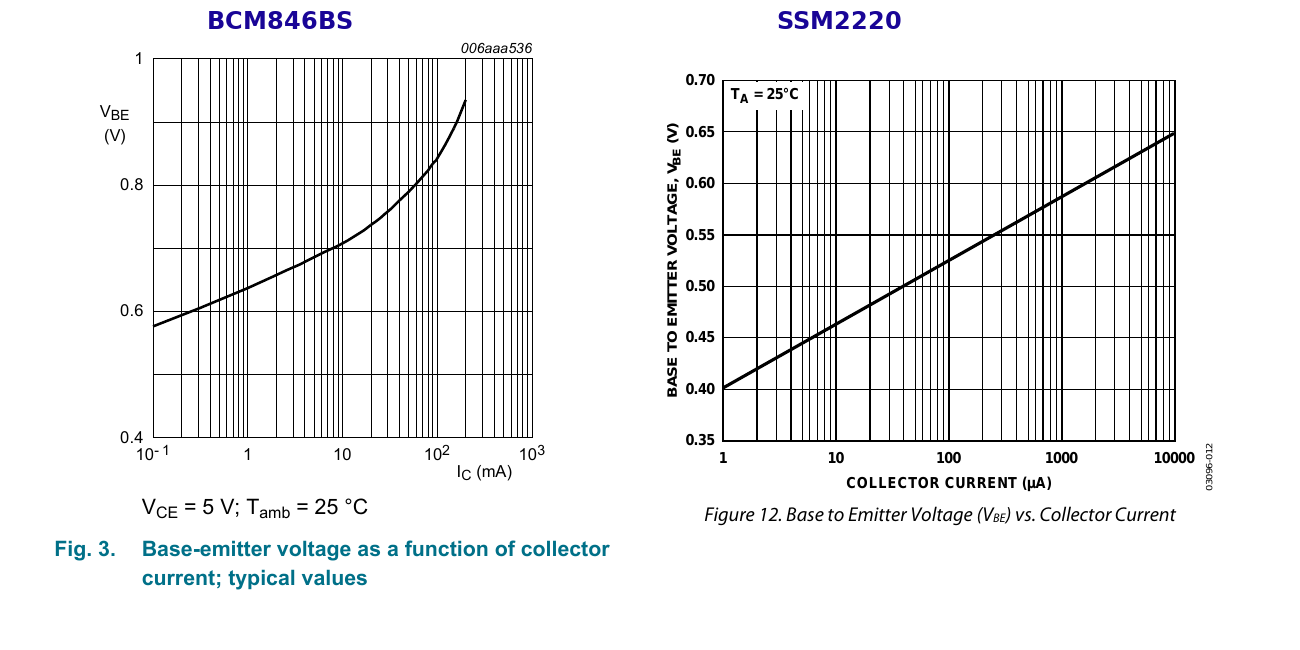
Die Diagramme aus Datenblättern für BCM846BS und SSM2220 zeigen für den Kollektor-Strom
eine logarithmische Skala, das Diagramm von LTspice zeigt absichtlich nur lineare Skalen.
Mit einer logarithmischen Skala ist der überwiegende Teil oder die gesamte Kennlinie
eine Gerade, weil die Kennlinie linear entsprechend gebogen verläuft.
Meist geht diese Gerade zu Beginn von höheren Kollektor-Strömen in eine leichte Biegung über.
Bei dem BC847C (Q1,Q2,Q3) ist das prinzipiell auch so.
Der Dual-Transistor SSM2220/SSM2212 (PNP/NPN) ist eine teure Besonderheit, der
in mehreren Hinsichten sehr hochgezüchtet ist.
Beispielsweise kann damit ein Logarithmier-Verstärker hergestellt werden.
| Zeit [µs] | Kollektor- strom [mA] |
BE-Spannung [mV] | Steilheit [mA/mV] |
Anstiegs- geschwind. [mA/µs] | BE-Spannung (Diagramm) [mV] |
|---|---|---|---|---|---|
| 40 | 0,07 | 429,4 | - | - | 294 |
| 50 | 0,228 | 432,565 | 20,03 | 0,3165 | 325,65 |
| 60 | 0,72 | 442,4 | 20,0 | 0,9835 | 423,9 |
| 70 | 2,11 | 464,1 | 15,6 | 2,17 | 641 |
| 80 | 5,32 | 510,0 | 14,3 | 4,59 | 1100 |
| 90 | 10,9 | 589,0 | 14,16 | 7,9 | 1890 |
| 100 | 18,57 | 711,0 | 15,9 | 12,2 | 3110 |
Eine Formel Ic(V) wurde entwickelt: Ic = 55e-6·e8,97·V
; e = 2,71828182846
Diese paßt im Mittelteil (..80..90..µs) der roten Stromkurve befriedigend.
Einheiten: A, V
19.Aug.2022
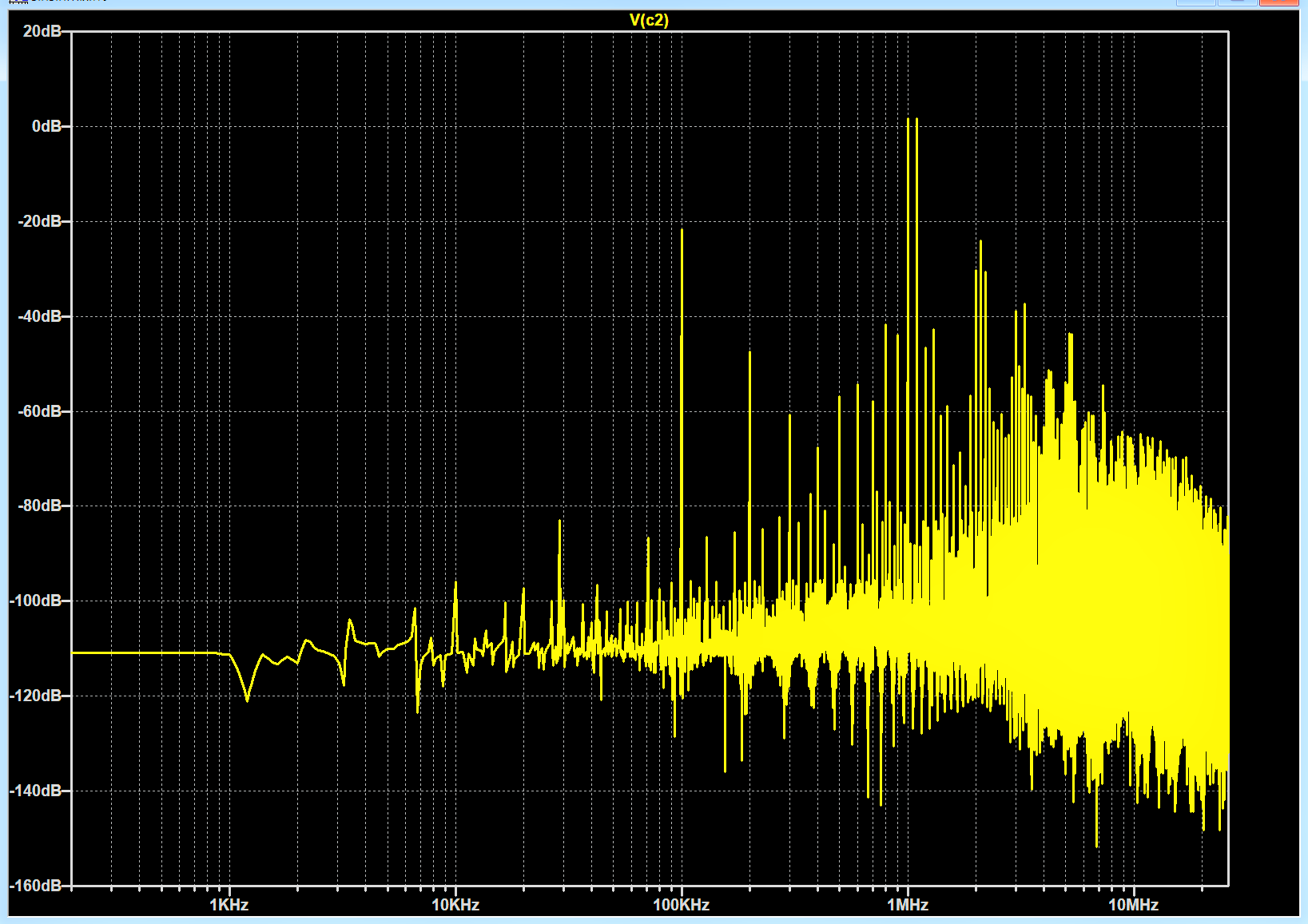
Beim Mischen von Sinus-Signalen entstehen die Differenz-Frequenz und die Summen-Frequenz. Die beiden Grundfrequenzen sind 1,0 MHz und 1,1 MHz. Folglich zeigt das vorstehende FFT-Diagramm die Grundfrequenzen, die Differenz-Frequenz 100 kHz, die Summe 2,1 MHz und viele weitere im Abstand von 100 kHz. Die Aufzählung beginnt mit der höchsten Amplitude, danach absteigende Amplituden. Diejenige Frequenz, die weiterverarbeitet werden soll, wird in der Regel steilflankig gefiltert, wodurch der Klirrfaktor des Signals stark sinkt.
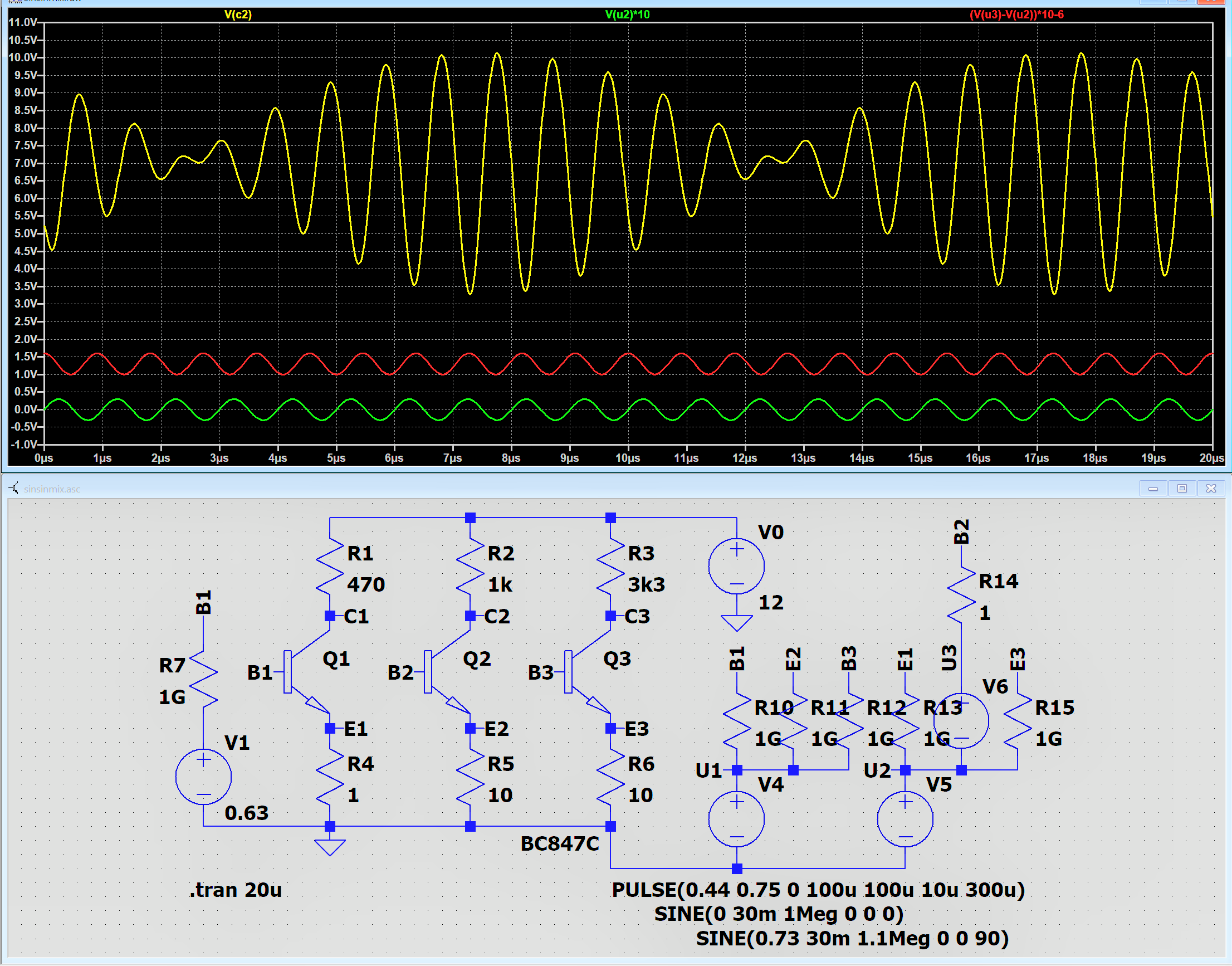
Von den drei Transistoren wird hier nur Transistor Q2 betrachtet und damit in Verbindung
stehende Bauelemente und Bezeichnungen.
Die grüne Kurve zu V(u2) und die rote zu V(u3) sind skaliert!
Die gelbe Hüllkurve des Mischsignals V(c2) hat eine Periodenlänge von genau 10 µs.
Das ergibt eine Frequenz von 100 kHz - die Differenz-Frequenz.
Eine gegenseitige Auslöschung der Grundwellen (1,0 MHz und 1,1 MHz) kann
es hier nicht geben, da deren Frequenzen ungleich sind.
Es ist erkennbar, daß die untere Kurve vor der darüber stehenden Kurve nach rechts flieht.
Deshalb hat sie die längere Periode und damit die geringere Frequenz.
Am Emitter-Widerstand fallen etwa 0,05 V ab, was den Offset von
V6 '0.73' entsprechend erhöht hat.
Die Spannungsverstärkung beträgt etwa 57, nicht 100, wegen 100=1k/10.
Das liegt an der Einstellung des Arbeitspunktes, der die Eigenschaft eines
Emitterfolgers nur stark eingeschränkt zur Wirkung kommen läßt.
Die zu mischenden Signale wurden mit ihrer kleinen Amplitude von 0,03 V
direkt hinein in die stark nichtlineare BE-Kennlinie gelegt.
Das produziert eine hohe Verstärkung und (anteilig) eine multiplikative Mischung, jedoch
große Verzerrungen und immensen Temperaturgang.
Eine bessere Lösung ist ein Doppelt balancierter Mischer mit drei Differenz-Stufen.
Die Spannungsquellen V5 und V6 zum Label B2 sind in Reihe geschaltet.
Dies kann für die Praxis nachgebildet werden, durch einen Summierer aus drei (vier) Widerständen,
der auf die Basis eines Emitterfolgers geht, dessen Emitter niederohmig mit B2 verbunden ist.
Siehe insbesondere den nachfolgenden Teil zum Thema.
20.Aug.2022
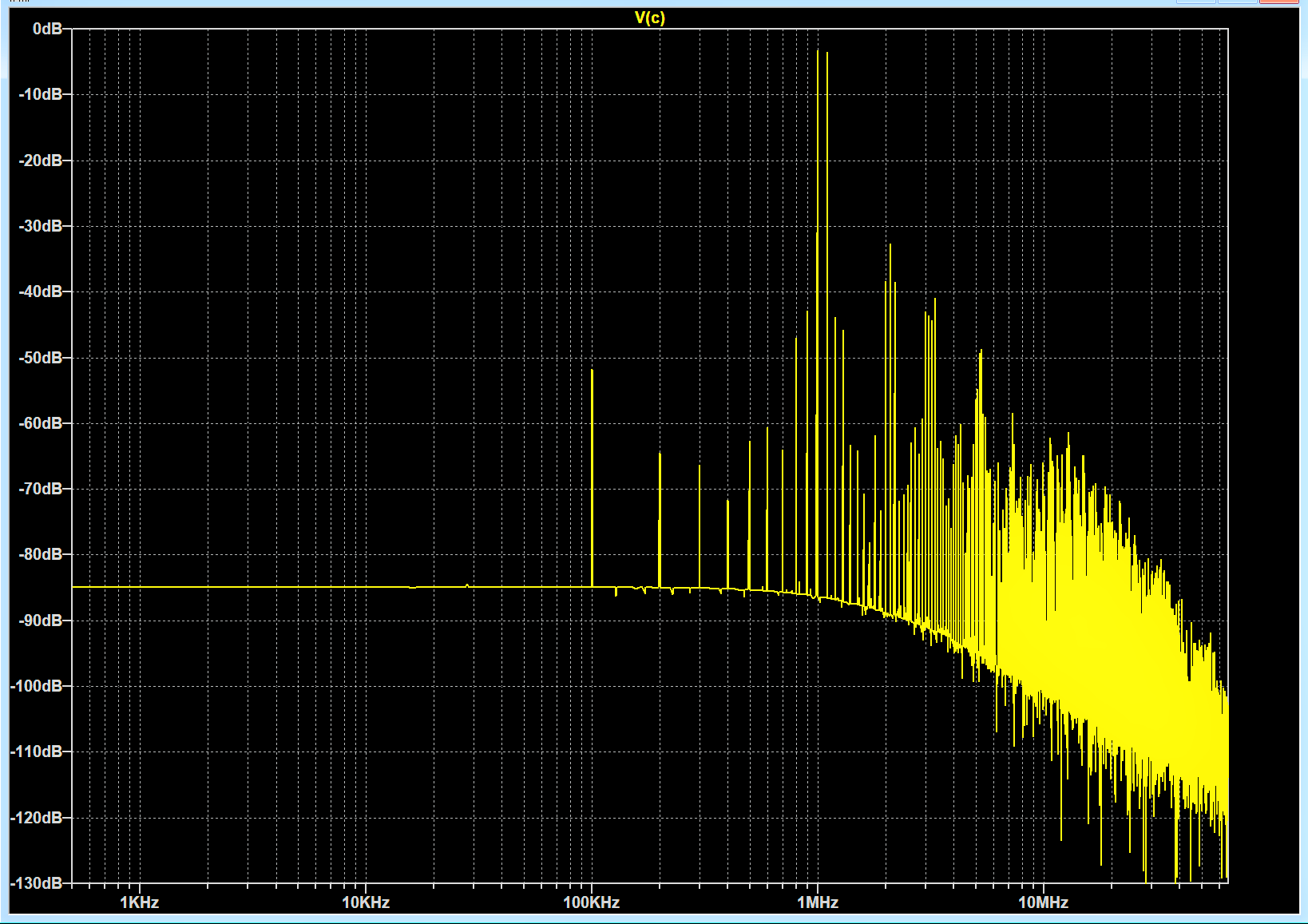
Gegenüber dem Diagramm unter der ersten Überschrift des Themas ist das Aufkommen an Frequenzen hier bedeutend geringer. Der Wust an Frequenzen ist stark ausgedünnt. Die Abstände zur Amplitude der Grundwellen sind beträchtlich größer. So hat die Differenz-Frequenz 100 kHz etwa 50 dB Abstand gegenüber etwa 23 dB Abstand (316 : 14). Das ist nicht überraschend.
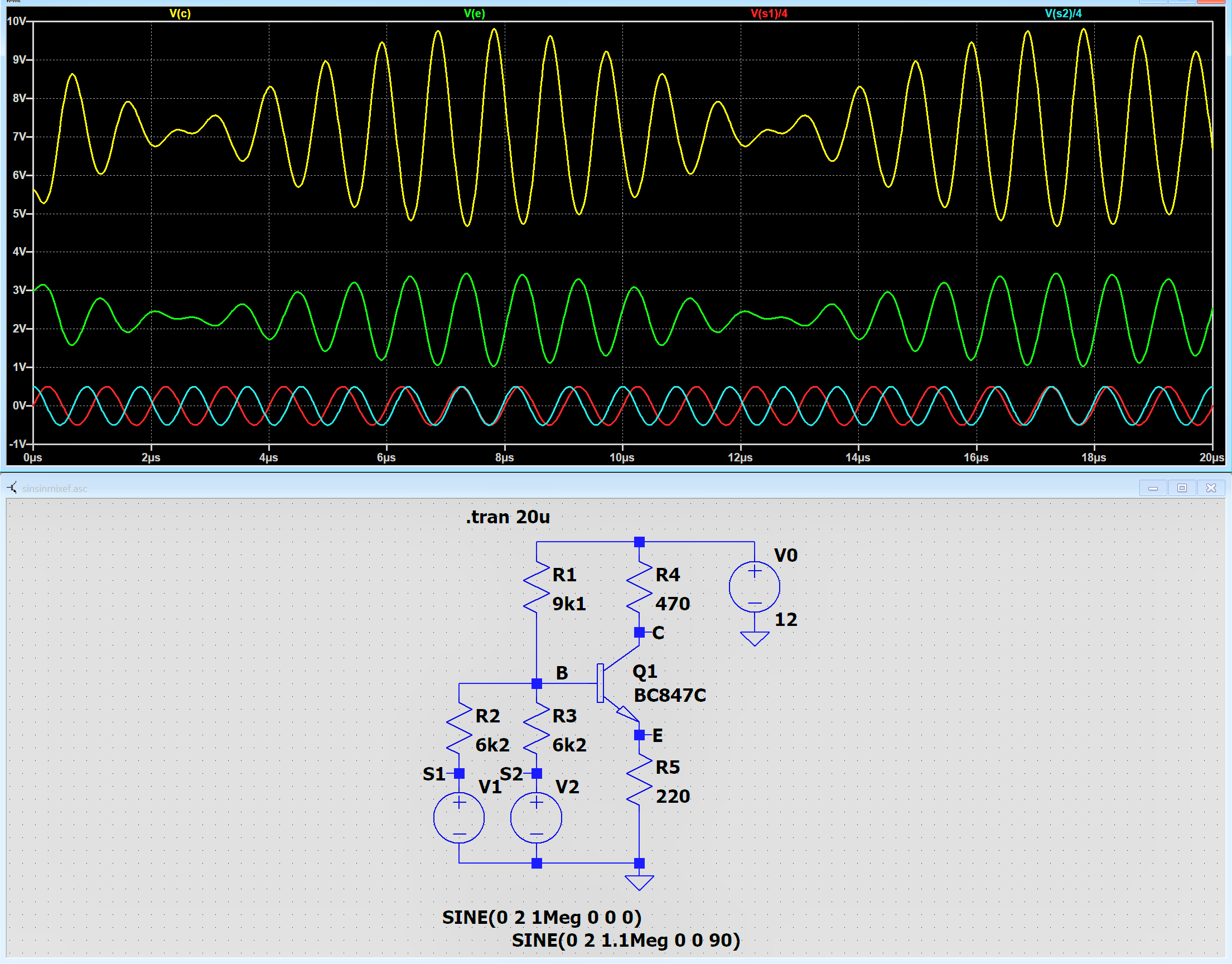
Vorstehend eine Schaltung, die eher ein Summierer denn ein Mischer ist.
Die beiden Signale S1 und S2 werden über R2 und R3 im R1 summiert und ohne
Verzerrungen auf die Basis (B) des Emitterfolgers Q1 gegeben.
Die Spannung am Emitter folgt derjenigen an der Basis und hat einen Stromfluß
durch den Emitter und R5 zur Folge, der zwangsläufig auch durch den Kollektor und R4 fließt.
(Der Basisstrom kann bei dieser Betrachtung vernachlässigt werden.)
Die Spannungsverstärkung ist mit etwa 2,13 gering (470/220).
Die Verzerrungen sind vernachlässigbar.
Wenn R4 auf 0 gesetzt wird, steigt V(e) von etwa 2,4 Vss auf etwa 2,8 Vss.
Es hat also einen geringen Einfluß, daß Uce zwischen 1,3 V und 8,8 V schwankt,
gegenüber einer Schwankung zwischen 8,6 V und 11 V.
R2 und R3 sind parallel geschaltet, wenn R1,R2,R3 als ein Spannungsteiler betrachtet werden.
21.Aug.2022
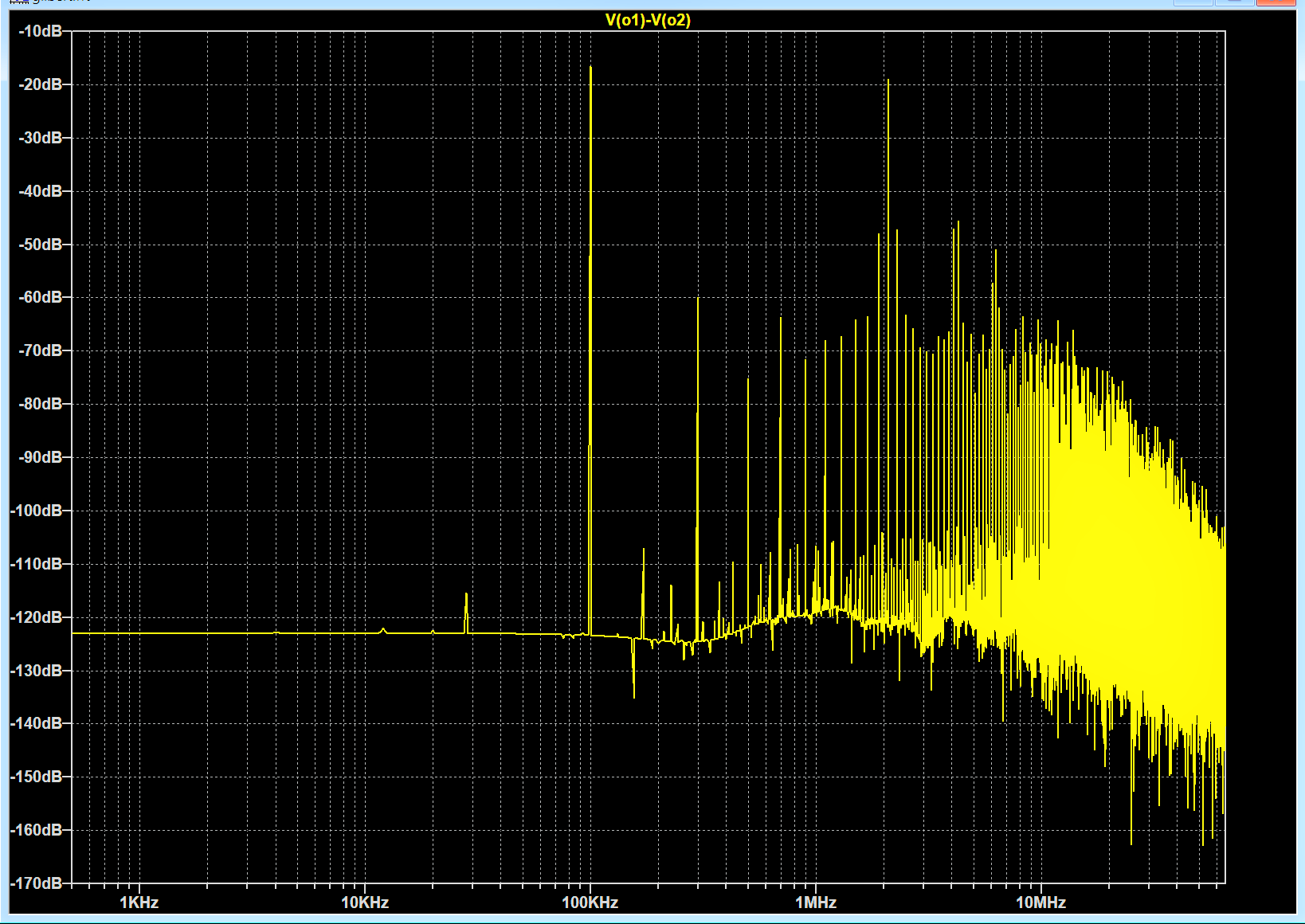
Hier, im dritten Abschnitt des Themas, sieht das Frequenzspektrum wieder ungefähr so aus wie im ersten Abschnitt des Themas. Es fehlen allerdings die Grundwellen (1 MHz und 1,1 MHz) und die geradzahligen Harmonischen der Differenz-Frequenz 100 kHz. Diese werden vom hier verwendeten Mischer unterdrückt. Vorhanden sind die Differenz-Frequenz und die Summen-Frequenz 2,1 MHz, und zwar mit auffallend großem Amplitudenabstand zum restlichen Frequenzaufkommen. Diese Eigenschaften kommen auch im Zeitdiagramm unübersehbar zum Ausdruck.
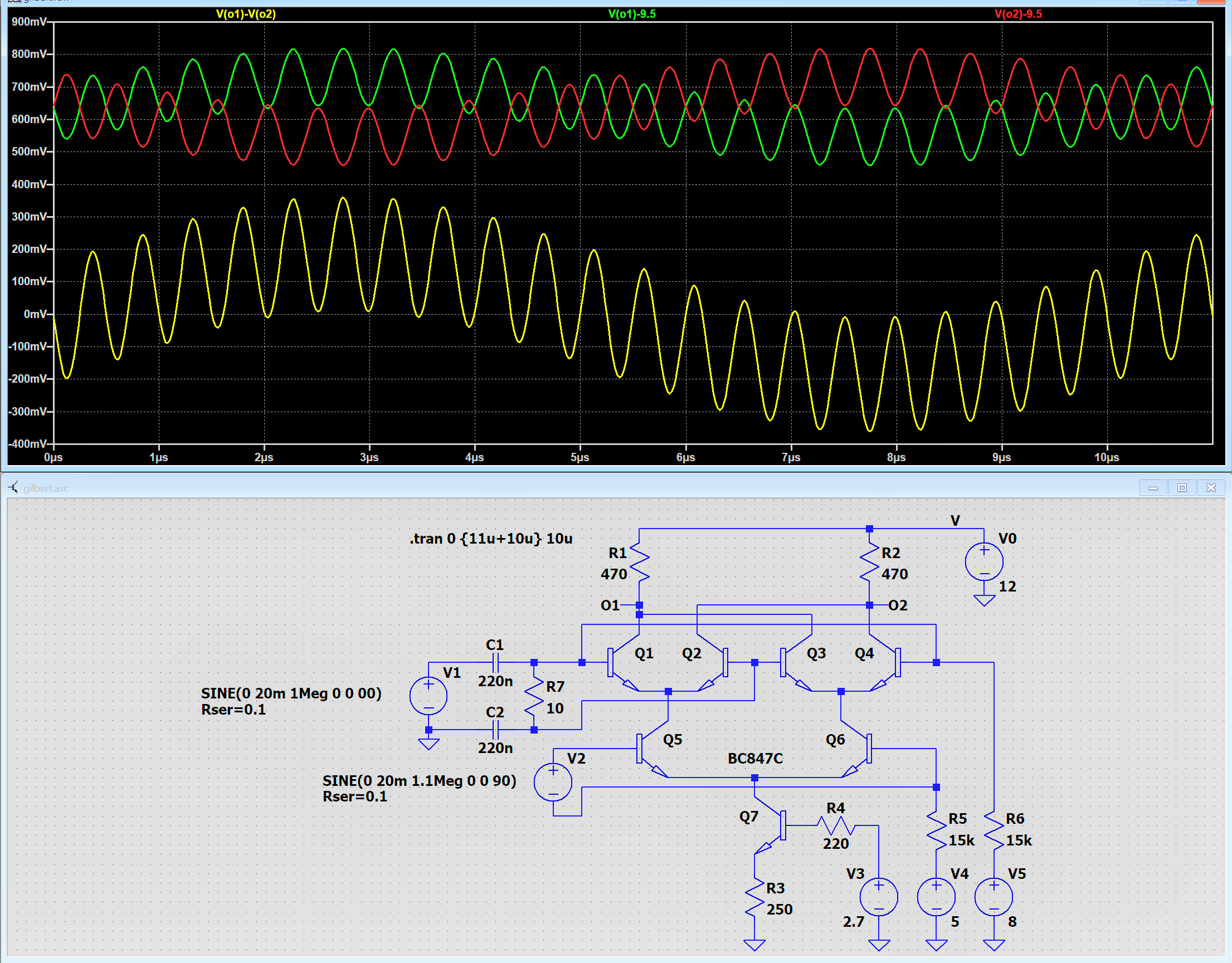
Als Mischer kommt hier die nach ihrem Erfinder benannte Gilbert-Zelle zur Verwendung.
Dies ist eine symmetrische Schaltung aus drei Differenz-Verstärkern und einer Stromquelle.
Kennzeichnend ist, daß die Eingangsspannungen direkt in die BE-Kennlinie hinein gelegt
sind, wie im ersten Abschnitt des Themas.
Hier sind die beiden Eingangsspannungen allerdings nicht in Reihe geschaltet, um in der
Kennlinie eines einzigen Transistors zu wirken.
Die Eingangsspannungen müssen deshalb in beiden Schaltungen klein sein.
Hier 2 × 20 mV, im ersten Abschnitt
30 mV + 30 mV.
Diese Schaltung multipliziert die Eingangsspannungen per Definition miteinander.
Es entstehen direkt die Differenz- und die Summenfrequenz, wobei die Signale
summiert/addiert erscheinen.
Die gemischten Grund-Signale sind am Differenz-Ausgang nicht sichtbar, sie sind unterdrückt.
Die Zeitskala hat deshalb auch 11 µs statt 20 µs als Endwert.
Die BE-Spannungen betragen im Arbeitspunkt 0,65—0,67—0,7 V.
Von oben nach unten betrachtet steigen diese Spannungen leicht an, weil immer
mehr Strom durch die einzelnen Transistoren fließt:
Durch R1 und R2 fließen je 4 mA. Anschließend 4 × 2 mA durch Q1,Q2,Q3,Q4.
Dann je 4 mA durch Q5 und Q6. Die Stromquelle Q7 führt schließlich 8 mA.
An R1 und an R2 stehen 2 V an. An den folgenden vier Transistoren 3 V.
Dann erneut 3 V. An Q7 2 V, und an R3 2 V Abfall.
Ergibt zusammen 12 V.
V2 ist eine schwebende Spannungsquelle (floating), die von der Wirkungsart
her einer galvanisch getrennten Wicklung einer HF-Spule entspricht.
V1 hingegen ist absichtlich eine normale unsymmetrische Spannung.
Deren Ankopplung bedeutet einen gewissen Aufwand.
Die Kondensatoren müssen relativ hochkapazitiv ausgewählt sein, weil der
niederohmige R7 für diese einen Lastwiderstand darstellt.
Der Widerstand 10 Ω muß ungefähr so niederohmig sein.
Immerhin hat dieser bei V2 (DC-mäßig) den Wert 0,1 Ω.
Es kann auch eine Differenzstufe (symmetrisch mit zwei Kollektoren) verwendet werden.
Die Signal-Spannung muß als Vorteil nur sehr gering sein, was einen niederohmigen Aufbau
einfacher macht.
Die Eingangs-Spannungen müssen floaten, weil es sonst eine Kollision
mit der Einstellung des Arbeitspunktes gibt (rechts unten).
Gleichzeitig müssen die jeweiligen Basen (quasi) kurzgeschlossen sein.
Bei V1 kann R7 (dann ≪ 10 Ω) mit einer Induktivität
in Reihe geschaltet werden. Das erhöht den Wechselstrom-Widerstand.
Resonanz-Erscheinungen müssen aber vermieden werden!
Praktikable Werte sind: 47 nF, 2 Ω, 30 μH.
Dies ruft vernachlässigbar kleine hochfrequente Verzerrungen hervor.
V(o1) und V(o2) wurden um 9,5 V nach unten verschoben.
R4, R5 und R6 sollen einen Eindruck von erlaubter Hochohmigkeit vermitteln.
Durch einen Dreifach-Spannungsteiler sollte 1 mA fließen.
Das Frequenzspektrum wurde mit schwebender V1 (wie V2) generiert.
12.Aug.2022
Beispielsweise kommt es vor, daß mittels Operationsverstärkern (OPV) Messungen
vorgenommen werden und bei bestimmten Meßwerten Signale von einem OPV-Ausgang zu
digitalen Logik-ICs (z.B. 74HC14: ≤ 6 V) direkt weitergegeben werden.
Also Spannungen bis etwa 36 V.
Oder ein Ausgang eines Meßgerätes soll ein Rechteck-Signal mit unbedingt
5··5,2 V Spannung
und geringer Impedanz ausgeben (z.B. 74ACXX).
In den vorstehenden Fällen und vielen weiteren werden Spannungsbegrenzer benötigt.
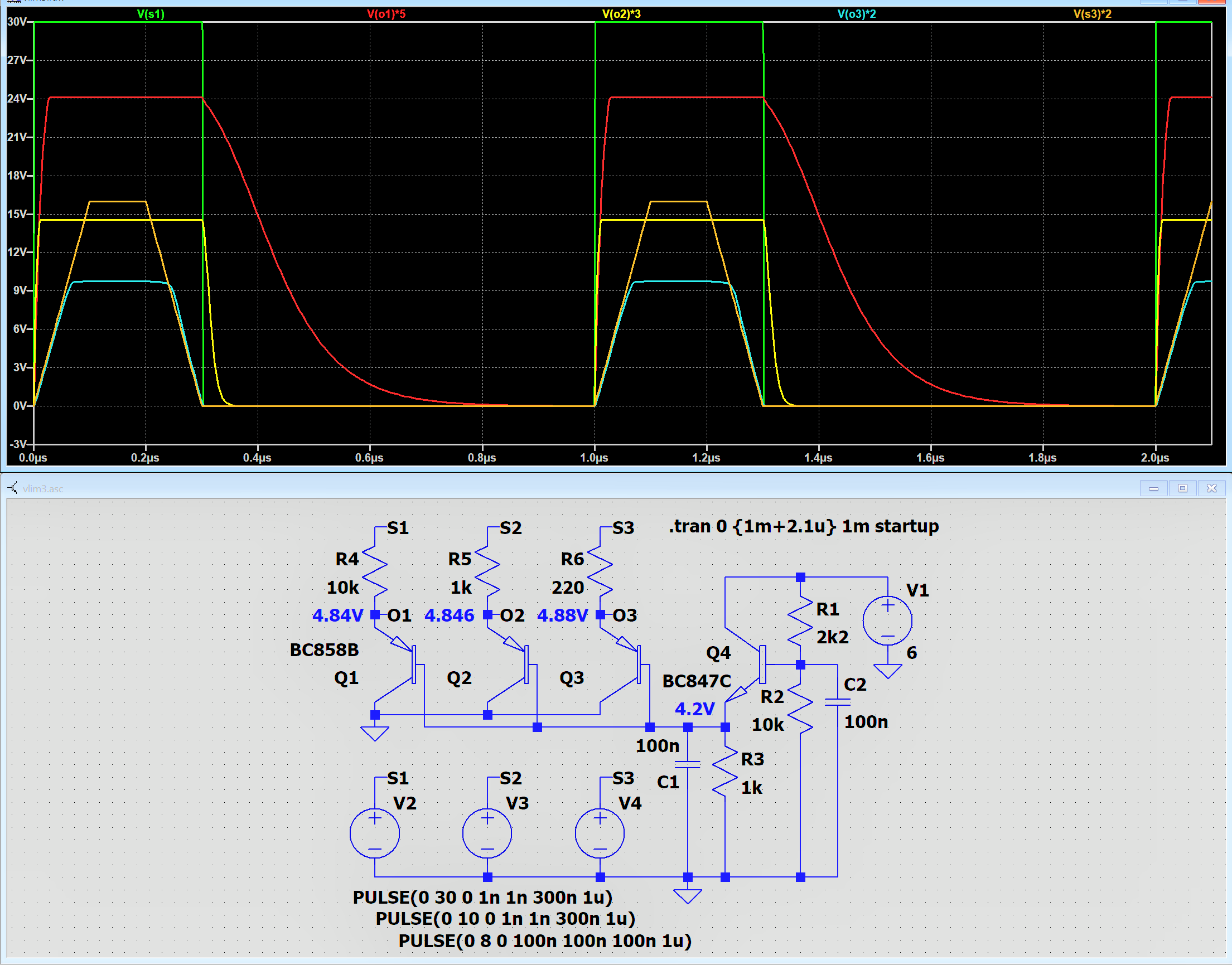
Die vorstehende Schaltung zeigt drei Begrenzer O1 O2 O3, die mit ihren
Basen mit ein und derselben festen Spannung (4,2V) verbunden sind.
Diese Spannung kann praktisch 100 solche Begrenzer versorgen.
Die Bauelemente Q4, C1, R3 können entfallen.
Der verbleibende Spannungsteiler und nötigenfalls weitere können Begrenzer mit
unterschiedlichen Begrenzungs-Spannungen versorgen.
Die Stütz-Kondensatoren können entfallen, falls die Ansprüche an solche Begrenzer
entsprechend geringer sind.
Alle Transistoren arbeiten in Basis-Schaltung, die hinsichtlich Hochfrequenz optimal ist.
Die Temperaturgänge zwischen PNP-Gruppe und NPN-Transistor heben sich gegenseitig auf, was
die Umgebungstemperatur angeht.
Unterschiedliche Leistungs- und damit Wärmeentwicklung in den Transistoren
machen diese Kompensations-Wirkung zumindest teilweise zunichte.
Ein geeigneter Aufbau auf Platine kann dies wiederum minimieren.
Die meisten Kurvenzüge im Diagramm sind durch Faktoren skaliert.
Die Spannung V(s3) ist trapezförmig.
Dadurch ist erkennbar, wie die ansteigende Spannung V(o3) ab etwa 4,4 V leicht
nach rechts abkippt, weil Q3 beginnt, merklich Strom, und immer mehr, nach GND abzuführen.
Bei horizontalem Verlauf von V(s3) (8V) ist dieses Verhalten gestoppt.
Die Begrenzer funktionieren sehr schnell.
Der langzeitige Abfall von V(o1) (rot) tritt in der Realität möglicherweise
abgeschwächt auf.
Ein Lastwiderstand 2k7 zwischen O1 und GND beseitigt diesen Spannungsverlauf.
R4 und dieser Widerstand bilden keinen Spannungsteiler, da R4 mit einer
großen Spannungsreserve an O1 geschaltet ist.
Erst herab auf 1.924k ≈ 4,84⁄[(30-4,84)⁄10k] fließt
kein Strom mehr in Q1.
ICs 74HCXX (ohne Schmitt-Trigger) vertragen eine Flankenzeit (tr,tf) von maximal 300 ns.
Dieses Limit wird hier eingehalten.
Anderenfalls müßte ein Schmitt-Trigger-Effekt verwendet werden.
Bei möglicher negativer Eingangsspannung sollte eine Diode zwischen
O# und GND geschaltet werden, mit Anode an GND.
06.Feb.2023
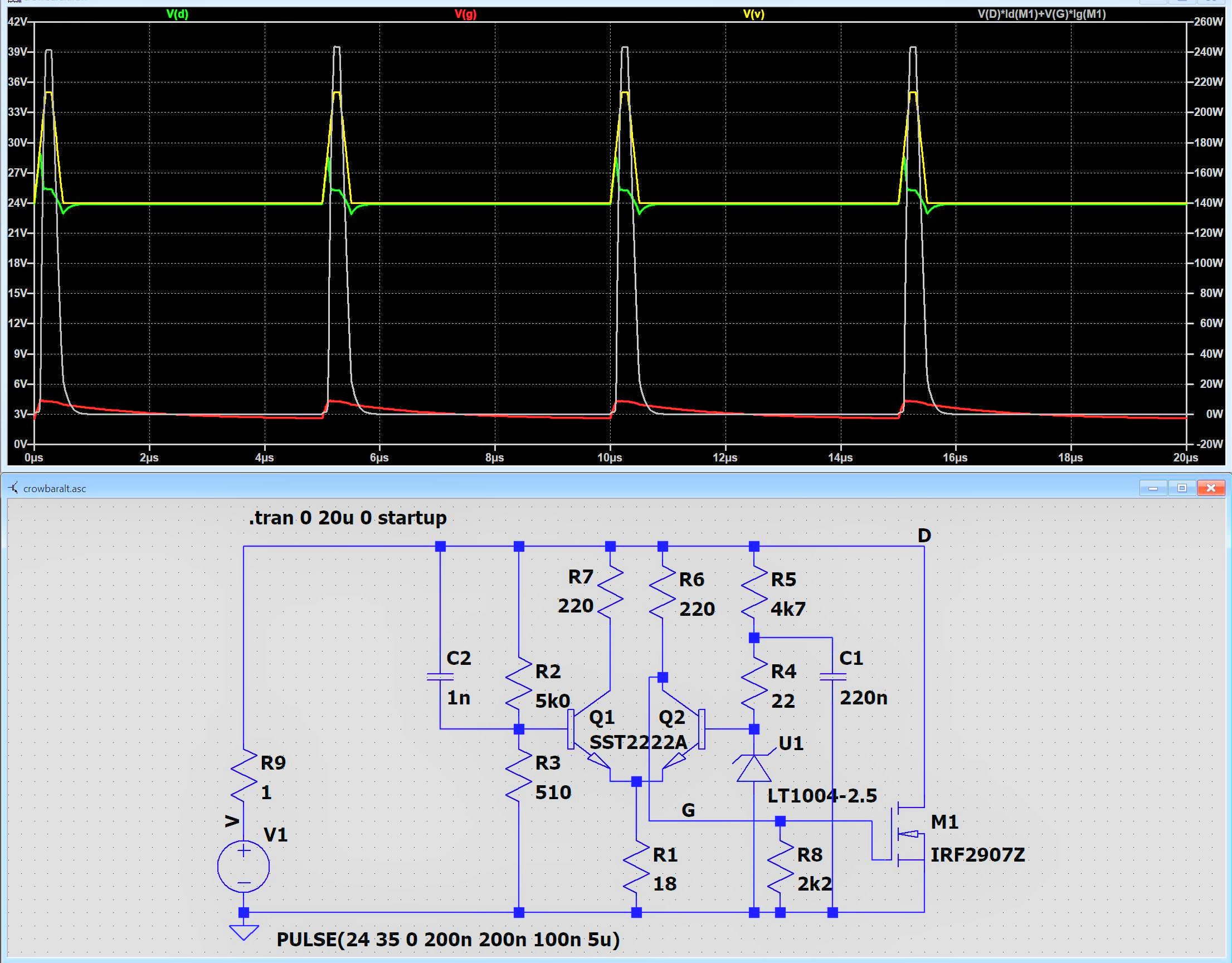
Eine Crowbar (Brechstange) ist eine Schaltung, die anmutet, als sei sie beispielsweise im Jahre 1967 erfunden worden, als es als verbreitete diskrete Bauelemente nur Bipolare NPN-Transistoren, Dioden, Zener-Dioden und Thyristoren (SCR) aus Silizium gab. Eine Crowbar soll an Betriebsspannung angeschlossene Schaltungen vor zerstörerischen Überspannungen (auf der Betriebsspannung) schützen. Dies geschieht durch das Zünden und dauerhaftes Durchschalten eines Thyristors, der absichtlich einen Kurzschluß verursacht, der eine Sicherung auslösen (durchschmelzen) soll. Es wird auch in Kauf genommen, daß durch diese Schutzfunktion eventuell die Stromversorgung (Netzteil) Schaden nimmt. Von dieser brutalen und rücksichtslosen Aktionsweise stammt auch der Begriff Brechstange.
Heutzutage werden solche Schutz-Schaltungen, die einen Service-Fall auslösen, in allen professionellen Bereichen unbedingt gemieden! In der Industrie, Medizinbereich, Militär, Luftfahrt, Weltraumfahrt, etc. Es ist nicht hinnehmbar, daß eine Schutzfunktion unnötig einen Ausfall einer gesamten Anlage oder eines Teils davon bewirkt!
Aus diesem Grund wird oben eine Schaltung präsentiert, die vorkommende Überspannungen gezielt eliminiert, und zwar nur, solange eine Überspannung (V) konkret anliegt! Außerhalb von Überspannungen macht diese Schaltung nichts - sie wartet nur. Die Schaltung funktioniert, indem sie bei Überspannung die Betriebsspannung durch einen Stromfluß belastet (M1), so daß eine Überspannung in nachfolgenden Schaltungen (D) gar nicht erst entsteht. Der Stromfluß bewirkt einen entsprechenden Spannungsabfall am Innenwiderstand (R9) der Betriebsspannung (V). Es handelt sich nämlich um einen stufenlosen Regler, nicht um eine Klemmschaltung.
Die Versorgungsspannung (D) für angeschlossene Schaltungen beträgt nominal 24 V. Üblich ist ein Funktionsbereich von 19 V bis 28 V. Die Schaltung ist so bemessen, daß sie 'D' ab 27 V begrenzt. Die Spannung 'D' schießt hoch bis 28 V, bewirkt durch eine Überspannung von 35 V mit schnellen Flanken auf 'V'. Die Leistungsspitze für M1 liegt bei 245 Watt. Mittelwert etwa 15 Watt.
Anstelle von LT1004-2.5 können auch LM385-2.5, TL431, etc. verwendet werden.
TL431 ist einstellbar und hat daher drei Anschlüsse.
Eine Besonderheit dieser Schaltung (und auch der Crowbar) ist die Genauigkeit
und Konstanz der Spannungsschwelle, ab der Überspannung erkannt wird.
Q1 gibt Leistung an R7 ab.
Die Body-Diode des MOSFET M1 verhindert negative Spannungen.
Die Spannung an R1 beträgt knapp 1,8 V, es fließt ein Strom von knapp 100 mA.
Der ist notwendig, um die Ansteuerung des Gate genügend niederohmig zu halten.
Die Gate-Kapazität Cgs beträgt nämlich bis zu etwa 25000 pF (oben 7500p).
Die Schaltung wurde schnell mit im Simulationsprogramm vorhandenen Modellen entwickelt und hat noch ziemlich viel Verbesserungspotential. Die drei Transistoren können noch besser ausgesucht werden. An die Emitter von Q1 und Q2 kann eine Stromquelle eingefügt werden. Die Ansteuerung des Gates (G) von M1 kann auch mit einem Kondensator (pos.&neg.) vorgenommen werden.
SiC-Trench-MOSFET (Familie, gleiches Gehäuse TO247-4) Infineon IMYH200R012M1H, IMYH200R075M1H, IMYH200R100M1H : 2000 V, 123 A kontinu., 2000 A^, 552 W, 9700 pF, 12 mOhm, tdon|tr|tdoff|tf = 16| 13|50| 24 ns @60A ... 2000 V, 34 A kontinu., 300 A^, 267 W, 1600 pF, 75 mOhm, tdon|tr|tdoff|tf = 7| 5|26| 7 ns @13A 2000 V, 26 A kontinu., 250 A^, 217 W, 1215 pF, 100 mOhm, tdon|tr|tdoff|tf = 2| 3|21| 5 ns @10A IMW65R030M1H: 650 V, 58 A kontinu., 240 A^, 197 W, 1643 pF, 30 mOhm, tdon|tr|tdoff|tf = 12| 11|20| 12 ns @30A IRF2907Z (s.o. Schaltung): 75 V, 170 A kontinu., 680 A^, 300 W, 7500 pF, 3.5 mOhm, tdon|tr|tdoff|tf = 19|140|97|100 ns @75A
Es ist erkennbar, daß ein optimaler Carbide-MOSFET eine starke Verbesserung nach sich ziehen würde.
Für den Differenzverstärker können damit kleinere und wesentlich schnellere Transistoren
verwendet werden, der MOSFET ist ebenfalls wesentlich schneller.
Ciss ist hier ein sehr wirksamer Parameter.
Erkennbar ist auch, daß die rise-time = 140 ns des verwendeten Modells
für das Mitschleppen der grünen Kurve V(d) verantwortlich ist.
10.Feb.2023, 16.Feb.2023
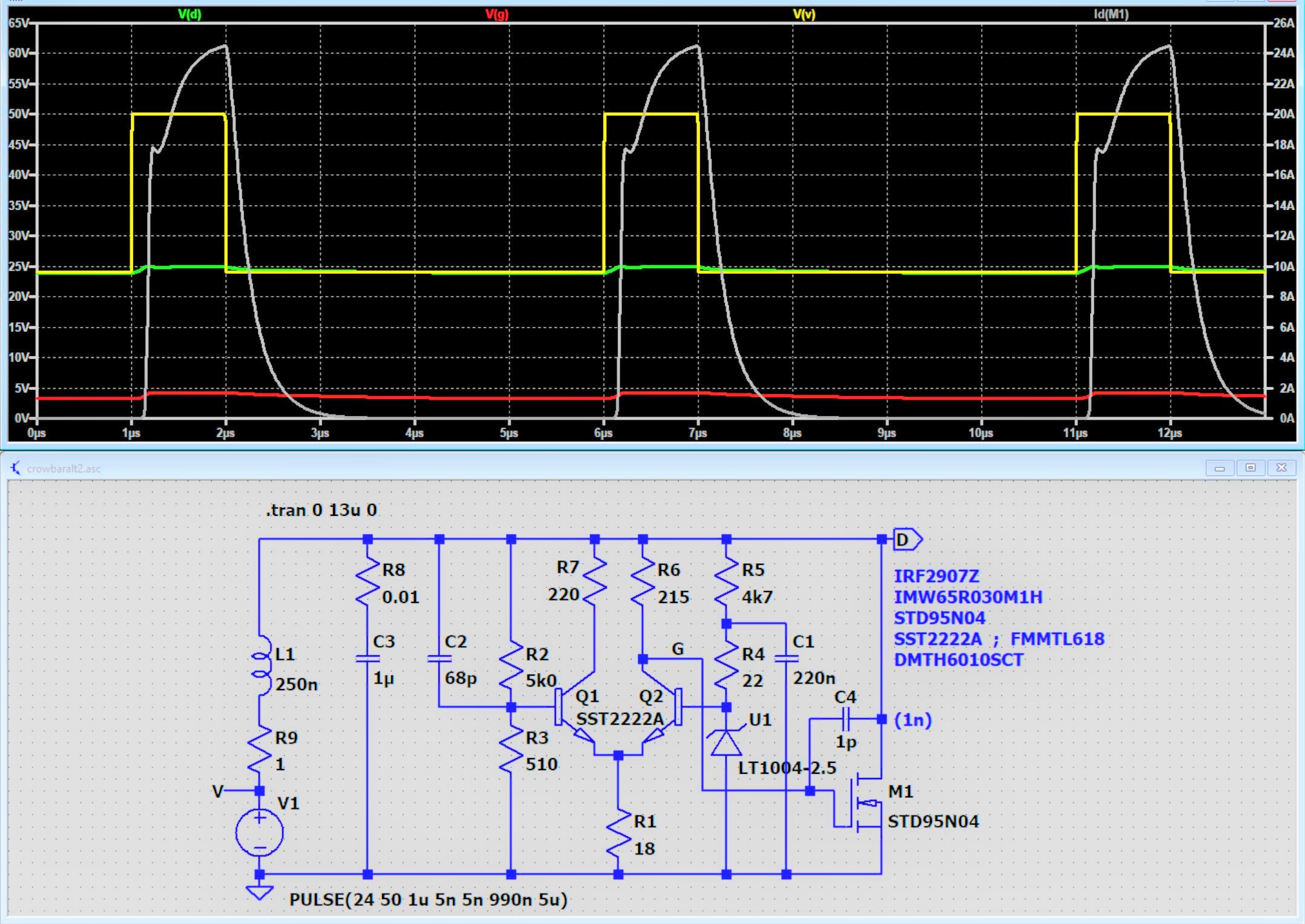
Die vorstehende zweite Version arbeitet sehr viel schneller.
Bewirkt hat das ein besser ausgewählter MOSFET
und eine genauere Einstellung des Arbeitspunktes des Differenzverstärkers.
Die Überspannung wurde von 35 V auf 50 V erhöht.
Die Anstiegs- und Abfallzeit wurden von 200 ns auf nun 5 ns
verkürzt! Allerdings vor dem Innenwiderstand R9; danach befindet sich
ein Kondensator C3 mit parasitärem Widerstand R8.
Dieser Kondensator macht durch seine Wirkung das Kurvendiagramm
inhaltlich merklich lebendiger.
Er reduziert die Flankensteilheit der Spannung D.
Auch die Induktivität L1 reduziert die Flankensteilheit.
L1 und C3 erleichtern der Schaltung ihre Arbeit erheblich!
Der Strom ID(M1) durch den MOSFET wird durch den Regler stets so gestaltet, daß
die Spannung V(d) (D) im gegebenen Rahmen optimal ist.
Die Reduzierungen der Flankensteilheit sind allerdings nicht erforderlich, damit
die Schaltung prächtig funktioniert.
Die Gate-Spannung beträgt maximal nur etwas mehr als 4 V.
Da ist (bis 20 V) folglich noch eine beträchtliche Reserve vorhanden.
Der MOSFET hat eine Steilheit von 100 A/V. Allerdings beträgt der Strom
bereits bei 7 V den theoretischen Wert von 250 A (Silizium).
Die Schaltung reagiert innerhalb von wenigen Nanosekunden vollständig, weil
sie sich ständig im Arbeitspunkt befindet.
Die Gate-Spannung muß lediglich um etwa 0,7 Volt größer werden, damit
der Strom von 0 A auf 30 A steigt.
Die Simulation wurde aus Gründen der Demonstration und optischen Erkennbarkeit den verwendeten MOSFET STD95N04 überfordernd eingestellt, durch die Einstellung der Spannungsquelle V1. Beispielsweise die Typen SCTW35N65G2V und STW48N60M2 sind geeignet, aber durchaus gefordert. Modelle für bessere Typen gibt es aber oft nicht, oder sie funktionieren in der benutzten Simulations-Software nicht.
Rolf Bombach hat einen Effekt an der Schaltung entdeckt, der auf der internen
Kapazität Cdg (Crss) des MOSFETs M1 beruht.
Die Kapazität kann durch einen externen Kondensator (C4) an Drain-Gate erhöht werden.
Eine solche Kapazität überträgt steilflankige Spannungsanstiege auf der
Betriebsspannung 'D' zum Gate und bewirkt einen sehr schnellen Anstieg
des Drain-Stromes.
Schneller, als es der Differenzverstärker kann.
Es handelt sich um eine wirksame Unterstützung des Differenzverstärkers
zu Beginn von Überspannungen.
Die Schaltung wurde von Rolf Bombach Killer-Miller genannt, weil
die Kapazität Cdg nach seinem Entdecker Miller-Kapazität genannt wird.
Die Wirkung von C4 = 1p ist vernachlässigbar;
der Wert 1 nF hat hingegen eine erkennbare Wirkung.
Die steil ansteigende Flanke des Stromes Id(M1) stammt von der Wirkung der
internen Miller-Kapazität Cdg.
Das Ende des steilen Anstiegs kennzeichnet das Ende der Wirkung des Cdg.
Diese Wirkung kann durch C4 verlängert werden.
Es wird unter diesem Thema hier ein Schaltungs-Konzept vorgestellt, welches durch eine beispielhafte funktionierende Schaltung demonstriert wird. Diese Schaltung muß hinsichtlich ihrer Werte und Typen an den jeweils konkreten Anwendungsfall angepaßt (und optimiert) werden. Es sind sicherlich 50 Varianten vorstellbar.
09.Feb.2023
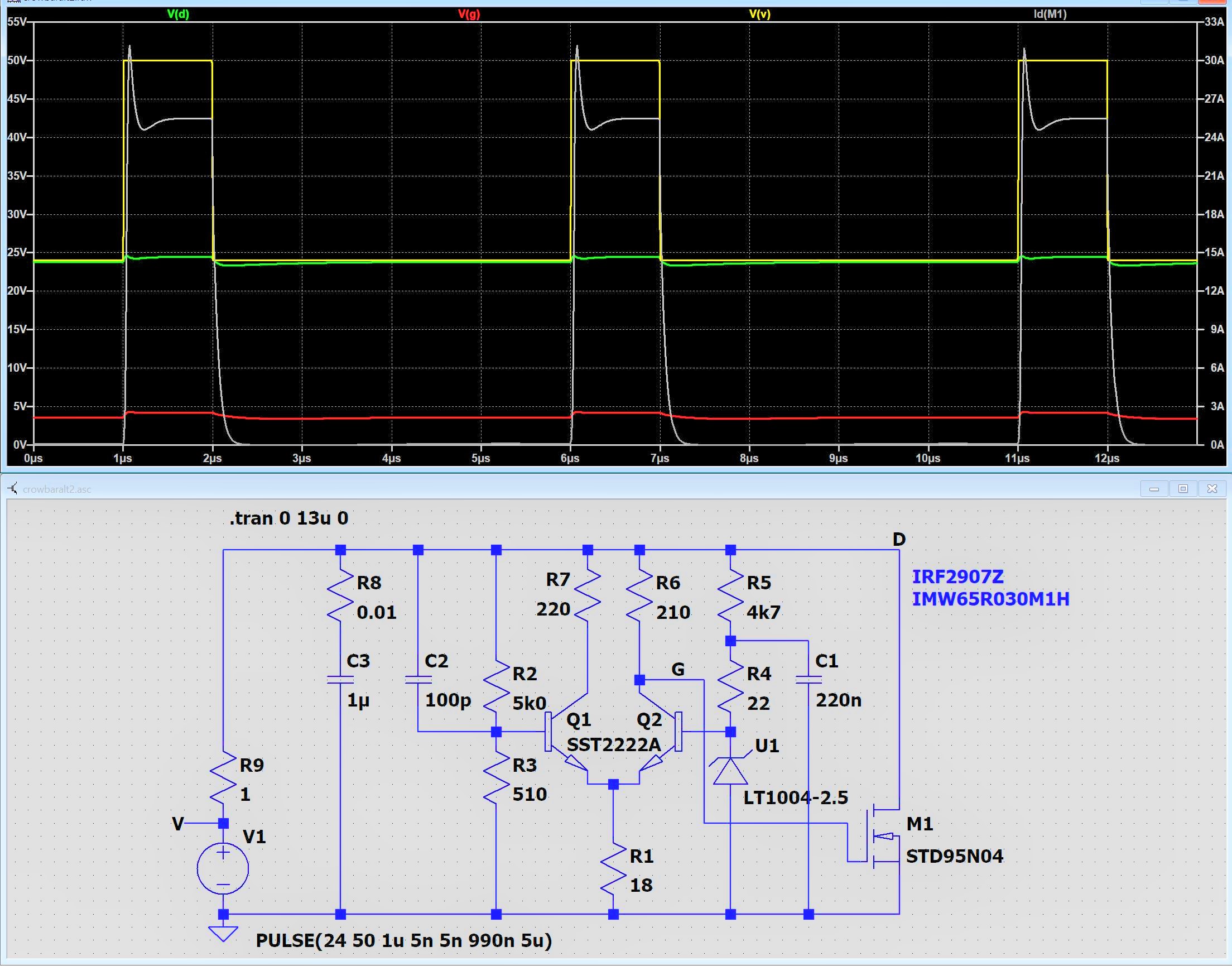
Vorstehend die Vorgänger-Schaltung ohne L1.
16.Feb.2023
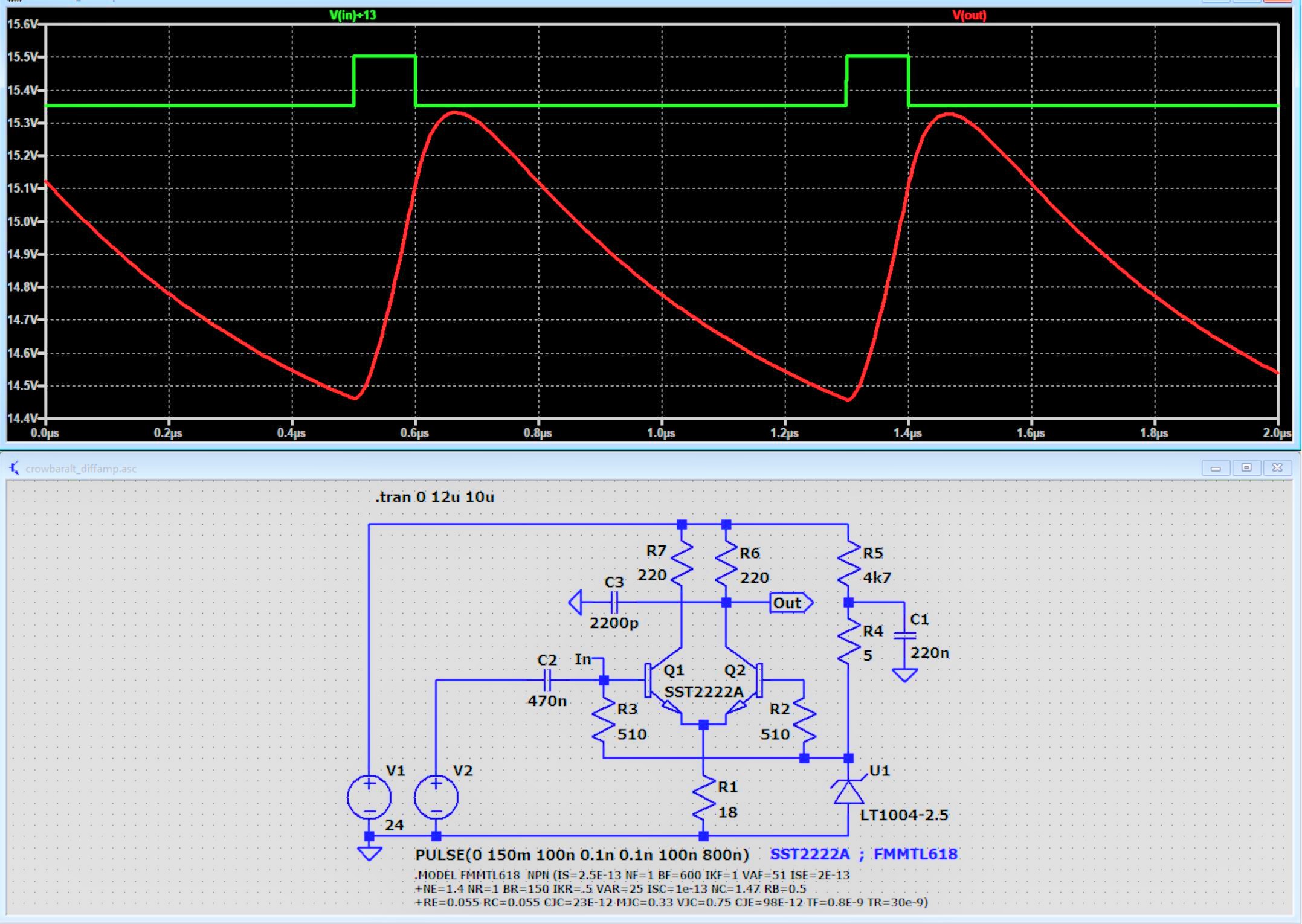
Vorstehend der separierte Differenz-Verstärker. Dieser arbeitet im gegebenen Rahmen recht schnell. Verstärkungsfaktor etwa 6 mit der gezeigten Beschaltung. Ohne die Lastkapazität C3 ist die Verstärkung etwa 25-fach. Der positive Ausgangsspannungshub kann im MOSFET innerhalb von 100 ns immerhin eine Stromsteigerung um etwa 40 A bewirken. Die Charakteristik des Verstärkers ist in den zugehörigen Schaltungen weiter oben erkennbar.
10.Dez.2020
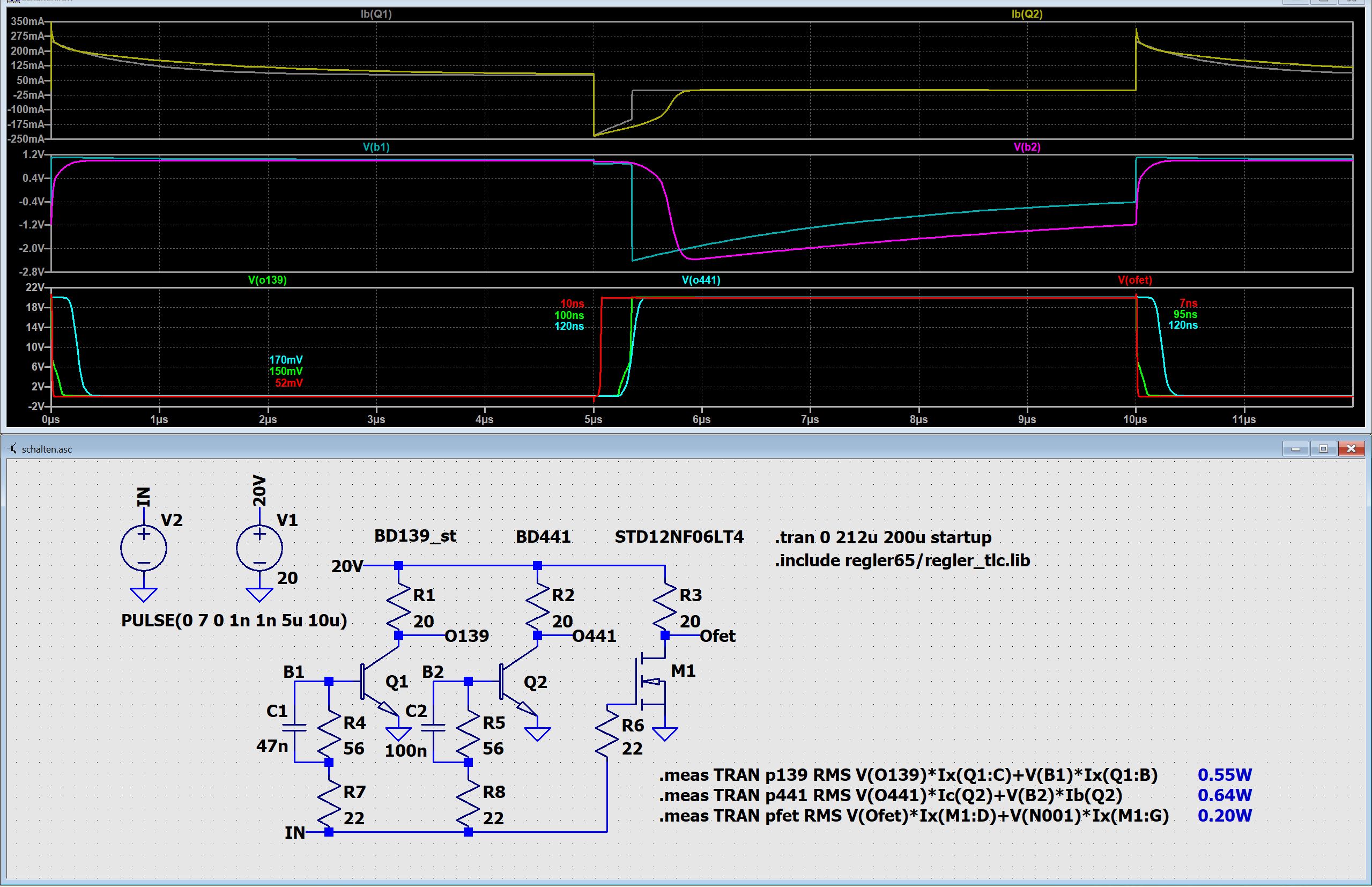
Vorstehend wird mit drei Transistoren (Medium-Power) ein Laststrom
von jeweils 1 A an 20 V geschaltet.
Es werden ausnahmslos Simulations-Modelle verwendet.
Das zuerst verwendete Modell für BD139 von ONsemi (MODPEX, www.i-t.com) ist
fehlerhaft, was an der seltsamen, Argwohn erregenden
Basisspannung V(b1)
erkennbar ist.
| Transistor | Parameter | Wert | Bedingungen |
|---|---|---|---|
| BD139 | Anstiegszeit | 95 ns | 10-90% |
| Abfallzeit | 100 ns | 10-90% | |
| Sättigungsspannung | 150 mV | – | |
| Wärmeverlustleistung | 0,55 W | – | |
| BD441 | Anstiegszeit | 120 ns | 10-90% |
| Abfallzeit | 120 ns | 10-90% | |
| Sättigungsspannung | 170 mV | – | |
| Wärmeverlustleistung | 0,64 W | – | |
| STD12NF06L-1 (MOSFET) | Anstiegszeit | 7 ns | 10-90% |
| Abfallzeit | 10 ns | 10-90% | |
| Sättigungsspannung | 52 mV | – | |
| Wärmeverlustleistung | 0,20 W | – | |
| FZT651 | Anstiegszeit | 3,6 ns | 10-90% |
| Abfallzeit | 6 ns | 10-90% | |
| Sättigungsspannung | 166 mV | – | |
| Wärmeverlustleistung | 0,23 W | – | |
| Verzögerungszeit, Speicherzeit: siehe Diagramme Einschalten: 20 V ↓ 0 V ; Schaltstrom: 1 A |
|||
Der BD441 verträgt immerhin 4 A dauerhaft und bewältigt 36 W im TO126.
Daher wirkt er träge im Vergleich zum BD139.
Ohne den relativ hochkapazitiven C2 versagt er praktisch völlig als Schalter.
Meister auf allen Ebenen ist der MOSFET im IPAK-Gehäuse, der 12 A dauerhaft
führen kann.
Er ist einer der kleinsten und schwächsten MOSFETs.
Deshalb hat er eine geringe Gate-Kapazität und dennoch einen
sehr geringen EIN-Widerstand.
Er übertrifft die beiden bipolaren Transistoren erheblich, ist aber
auch ein ausdrücklicher Schalttransistor.
(Preis ca. 1 € bei 1 Stück.)
Es geht hier um ein kompromißloses Schalten, um eine sehr geringe Sättigungsspannung zu erreichen. In Datenblättern ist es üblich, hierfür Ib = Ic / 10 zu wählen. Beispielsweise bei digitalen Gattern kann eine geringe Sättigung angestrebt werden - hier jedoch nicht! Gleichzeitig sollen natürlich alle Schaltzeiten optimal kurz sein. Dazu sind C1 und C2 vorhanden, die u.a. eine negative Basis-Emitter-Spannung bewirken, um Ladungsträger auszuräumen.
^Ein sehr guter bipolarer Transistor FZT651 wurde hinzugefügt. Dazu sind keine Diagramm-Bilder vorhanden. Dessen Flankenzeiten sind sehr klein. Die Verzögerungszeiten sind wie bei den BDXXX. C2 konnte hier auf 47 nF reduziert werden. Der Spannungsverlauf am Ausgang ist rechteckig wie beim MOSFET. Der MOSFET hat dennoch die geringste Verlustleistung, wegen seiner geringen Sättigungsspannung. Weiterhin fällt er mit seinen sehr geringen Verzögerungszeiten auf.
25.Dez.2020
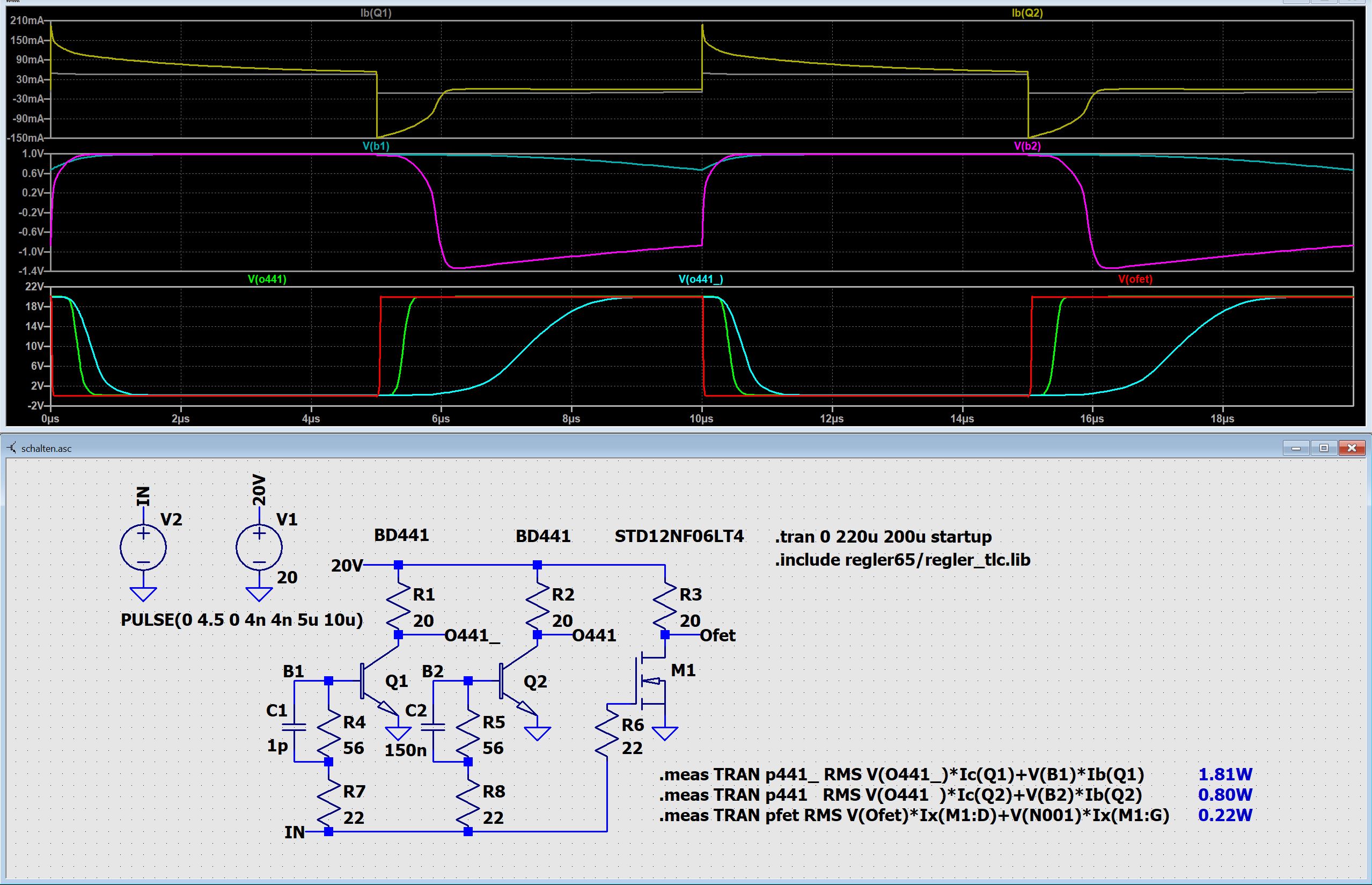
Der Transistor BD441 wurde ohne (1 pF) und mit (150 nF) Beschleunigungskondensator verglichen. Die Wirkung ist gewaltig, wie die Kurvendiagramme und die Verlustleistungen (rechts unten) zeigen. Die Widerstandswerte blieben unverändert. Verändert wurden die Puls-Spannung 7 V → 4.5 V und die Flankenzeiten 1 ns → 4 ns, um zu demonstrieren, daß der MOSFET auch mit deutlich geringeren Gate-Spannungen voll und schnell durchsteuert. Ein Rg = 330 R ändert nicht viel daran. Bewirkt dadurch, daß der MOSFET eine geringe Gate-Schwellwertspannung von typ. 1,5 V und eine hohe Steilheit von etwa 17 A/V hat. Die Gate-Kapazität beträgt lediglich 350 pF.
Als Fazit kann gezogen werden, daß für bipolare Transistoren die gezeigte Schaltung mit den beiden Widerständen und dem Kondensator summa summarum die beste ist. Als Schalttransistor sollte ein MOSFET herangezogen werden. Auch, weil es dafür integrierte leistungsfähige Treiber gibt, auch im SOT23-Gehäuse. Diese haben CMOS+TTL-kompatible Eingänge, Schmitt-Trigger und Ausgänge aus komplementären MOSFETs, die etwa 1 A bis 30 A Pulsstrom vertragen. Besonders bekannt für solche Produkte ist der Hersteller IXYS.
28.Dez.2020
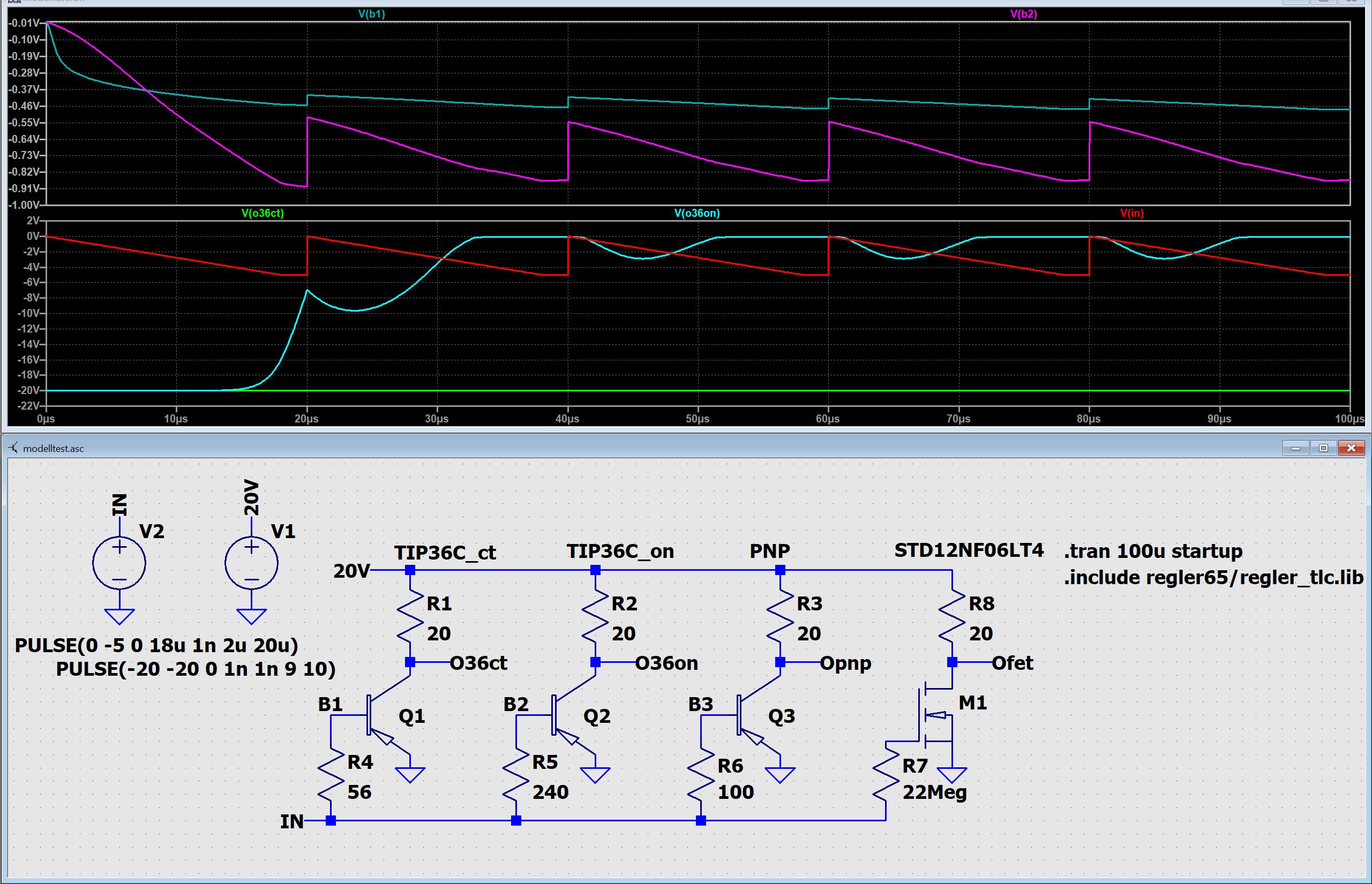
Vorstehend auf dieser Webseite wurden bereits fehlerhafte Spice-Modelle entdeckt
und besprochen.
Hier nun eine Möglichkeit zur systematischen Erkennung.
Es wurden zwei verschiedene Modelle für den selben Transistor-Typ
TIP36C mittels geeigneter Simulation verglichen.
Ein Modell hat sich mit Hilfe der Testschaltung sofort als massiv
fehlerhaft herausgestellt, nämlich das von CentralSemiconductor (_ct).
Das von ONsemi (_on) ist brauchbar, was nicht heißt, daß es makellos ist.
Denn von ONsemi ist das Modell für BD139 grob fehlerhaft, während das Modell
von ST für den selben Transistor-Typ brauchbar ist (BD139_st).
Die beiden Kollektor-Spannungen zeigen sofort aufgrund ihrer völligen
Unterschiedlichkeit ein fehlerhaftes Modell an [V(o36ct), V(o36on)].
Unterstützt wird das durch die beiden stark unterschiedlichen
Basis-Spannungen V(b1) und V(b2).
Der jeweils erste Graph zeigt auch absolut betrachtet ein Verhalten, das
ein bipolarer Transistor gar nicht haben kann.
Die Kollektor-Spannung
Die Testschaltung wurde so ausgelegt, daß sie insbesondere das Analoge
eines Transistors zeigt.
Die Kennlinien sollen sichtbar komplett durchlaufen werden.
Das brauchbare Modell generiert typische Verläufe.
Es ist das Verhalten eines steuerbaren Transistors erkennbar.
Die Ansteuerung per R4 und R5 wurde so gewählt, daß die Stromverstärkung
gerade eben zum Durchsteuern ausreicht.
Transistor Q2 (_on) will nach Abschalten der Eingangsspannung V(in) nach
seiner Speicherzeit sperren, wird aber dabei von der wieder ansteigenden
Eingangsspannung überholt.
Obwohl der Wert des R4 von 240 Ω auf 56 Ω beträchtlich
reduziert wurde, reagierte die Kollektor-Spannung des Q1 (_ct) darauf nicht.
Laut Datenblatt ist der TIP36 ein ausdrücklicher Power-Transistor:
25/40A, 100V, 125W, hFE=120@≤2A.
Komplementär ist TIP35 (NPN).
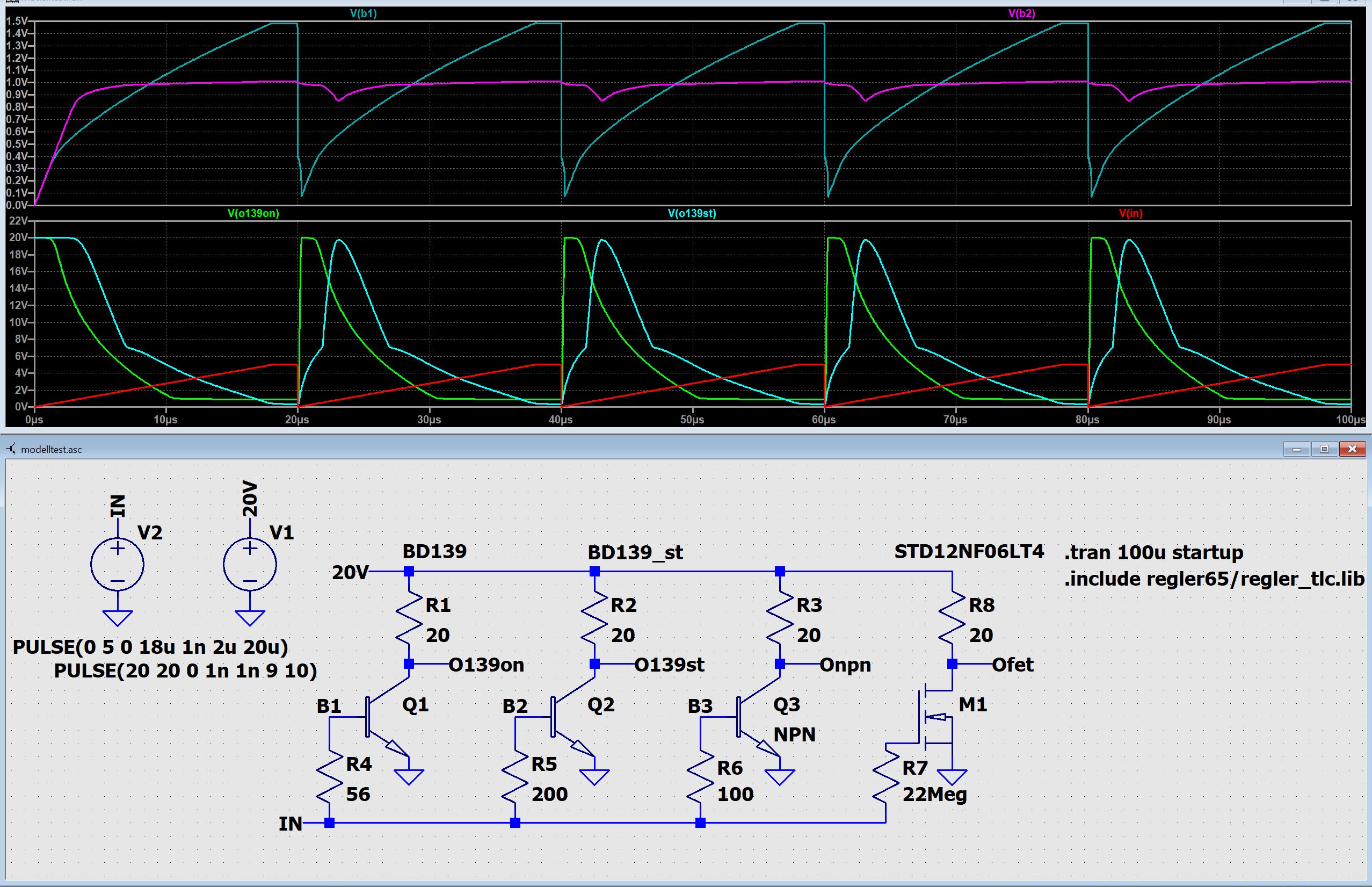
Hier wurden zwei Modelle für den Typ BD139 verglichen.
Das erste Modell (links, grün,
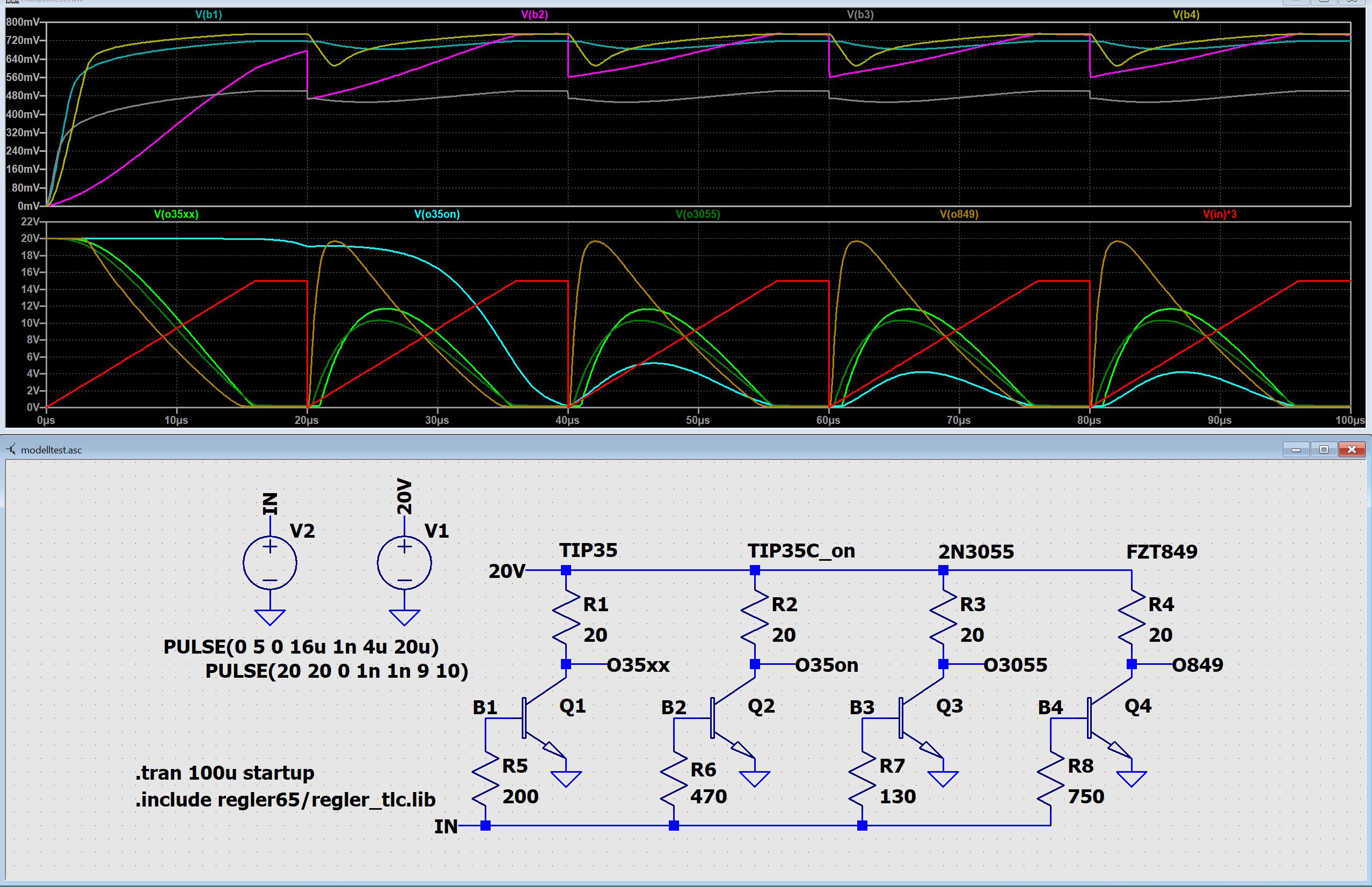
Vorstehend ein Bild, welches einen Vergleich zweier Modelle für den
Transistor-Typ TIP35 zeigt.
Zusätzlich wurden aus der Library von LTspice die Typen 2N3055 und FZT849 angefügt.
Die Modelle sind unten angegeben.
Keines der Modelle weist einen groben Fehler auf.
Alle diese Modelle sind verwendbar.
Das erste Modell hat 23, das zweite 40 Parameter.
Fehlende Parameter werden durch Default-Werte ersetzt.
Es ist erkennbar, daß alle Modelle steuerbare Transistoren generieren.
Unterschiedliche Stromverstärkung (BF) wurde durch unterschiedliche Werte
für R5 .. R8 berücksichtigt.
Dabei wurde in einer solchen Weise justiert, daß vor dem Ende einer Periode
eine geringe Sättigungsspannung erreicht ist.
Auffallend sind mehrere Unterschiedsarten bei den Basisspannungen:
spitzeckig, abgerundet, Mittelwert, Delta.
Die niedrige Basisspannung des Q3 wird durch seine stromstarke Basis in Verbindung
mit geringer Stromverstärkung begründet sein.
Q4 reagiert offensichtlich sehr schnell auf Änderung seines Basisstroms.
Er ist mit Abstand der hochfrequenteste Typ.
Q2 fällt mit seiner wirklich extrem trägen Ausgangsspannung auf.
Das ist wohl nicht in Ordnung so, und in der Realität nicht vorhanden.
Dieses Verhalten kann eine Folge von Parameter-Werten sein, die zu sehr
vom jeweiligen korrekten Wert abweichen.
Es wird nochmals darauf hingewiesen, daß die ersten beiden Modelle
für den selben Transistor-Typ gemacht sind.
Angesichts dessen weisen die hier vorliegenden starken Unterschiede
auf eine schlechte Zusammenstellung von Parameterwerten hin.
Den besten Eindruck hinterließen bisher Modelle von Diodes und TI
(LTspice außen vor.).
Normalerweise werden Exemplar-Streuungen von Transistoren schaltungstechnisch
durch allerlei Gegenkopplungen wirkungsmäßig eliminiert, so daß Schaltungen
vorausberechenbar werden und unabhängig von Streuungen stets gleiches
Verhalten zeigen - mit nun auskömmlichen Streuungen.
Simulationen verwenden bei Modellen typische Werte.
Jedoch ändert das gar nichts an den allgemeinen schaltungstechnischen Maßnahmen.
In diesem Artikel jedoch wird das Gegenteil getan!
Unterschiede sollen deutlich hervortreten, damit Analysen möglich werden.
Dieses Konzept hier muß berücksichtigt werden.
Oft wird kolportiert, Simulationen seien u.a. wegen der realen Streuungen der Bauelemente unsinnig, mit ungültiger Aussage. Das ist falsch und unlogisch! Korrekt ist, daß die Qualität von Simulationen von der Qualität der Modelle und vom Aufwand beim Aufbau der Simulation abhängt. Eine Simulation kann prinzipiell der Realität zu 100% entsprechen! In der Praxis von Simulationen gibt man sich lediglich nicht die dafür erforderliche Mühe. Diese ist auch tatsächlich meist vernachlässigbar. Beispielsweise umfangreich bei NF-Schaltungen. Allein auf dieser Webseite gibt es Simulationen, die reale elektronische Geräte, die vor Jahrzehnten entwickelt und aufgebaut wurden, in ihren Daten und Eigenschaften bestätigen: z.B. Netzgerät, Oszillator GT, Oszillator L3. Auch das ganze damalige Entwicklungsverhalten der Schaltungen spiegelt sich in der Simulation wieder. Die Simulation mit ihren Modellen muß dazu lediglich gut genug sein - dann wird die Realität (genügend) abgebildet.
.MODEL TIP35 NPN (IS=1.84e-12 NF=1 BF=81.5 VAF=161 IKF=8.33 ISE=1.97e-9 NE=2 +BR=4 NR=1 VAR=20 IKR=12.5 RE=13.2e-3 RB=53e-3 RC=5.3e-3 XTB=1.5 +CJE=801e-12 VJE=.6 MJE=.3 CJC=520e-12 VJC=.22 MJC=.2 TF=54.1e-9 TR=2.08e-6) .MODEL TIP35C_on npn( +IS=7.88586e-11 BF=256.257 NF=0.951481 VAF=25.9112 +IKF=6.91656 ISE=6.4e-12 NE=3.4 BR=4.49993 +NR=1.08286 VAR=4.40924 IKR=3.69854 ISC=3.9e-13 +NC=3.99 RB=20.929 IRB=0.1 RBM=0.135255 +RE=0.000998231 RC=0.0563125 XTB=0.1 XTI=1 +EG=1.10826 CJE=1e-07 VJE=0.421306 MJE=0.693953 +TF=1e-08 XTF=1.35777 VTF=1.00063 ITF=0.9994 +CJC=5e-10 VJC=0.400277 MJC=0.409924 XCJC=0.803124 +FC=0.720291 CJS=0 VJS=0.75 MJS=0.5 +TR=4.99888e-07 PTF=0 KF=0 AF=1) .model 2N3055 NPN(Bf=73 Br=2.66 Rb=.81 Rc=.0856 Re=.000856 CJC=1000P +PC=.75 MC=.33 Tr=.5703U Is=2.37E-8 CJE=415P PE=.75 ME=.5 TF=99.52N +NE=1.26 IK=1 Vceo=60 Icrating=10 mfg=STMicro) .model FZT849 NPN(IS=5.8591E-13 NF=0.9919 BF=230 IKF=18 VAF=90 +ISE=2.0067E-13 NE=1.4 NR=0.9908 BR=180 IKR=6.8 VAR=20 ISC=5.3E-13 +NC=1.46 RB=0.023 RE=0.0223 RC=0.015 CJC=200E-12 MJC=0.3006 VJC=0.3532 +CJE=1.21E-9 TF=1.07E-9 TR=9.3E-9 Vceo=30 Icrating=7 mfg=Zetex)
Leider sind Modelle oft nachlässig, auch fehlerhaft erstellt, wie es dieser Artikel ja ausdrücklich vorführt. Beispielsweise sind oft fast alle Parameter beim komplementären Typ exakt gleich. Die Realität trifft das sicher nicht. Eine Reparatur eines Modells blauäugig vorzunehmen würde wahrscheinlich zu einem Mißerfolg führen. Es muß damit gerechnet werden, daß jeweils mehrere Parameter untereinander in komplexer Weise voneinander abhängen. Auch möglich ist, daß bei der Erstellung eines Modells eine bestimmte Linie verfolgt wurde. Es können Parameter vermeintlich abweichende Werte haben, was jedoch Absicht sein kann. Reparaturversuche können alles schlimmer machen, als es bereits ist (herumgedoktort). Entweder, es werden gute Modelle beschafft, oder man selbst muß Modelle von Grund auf sorgfältig herstellen, nach intensivem Lernen des dazu Notwendigen.